|
appunti di un viaggio da Euclide a Einstein. Giorgio Ottaviani Dipartimento di Matematica. via Vetoio, Coppito, 67010 L'Aquila ottavian@univaq.it In ricordo di Eugenio Banzi
§1. UNA FORESTA EUCLIDEA Il nostro viaggio comincia, seguendo le parole di Einstein, dal "superbo edificio della geometria euclidea". Se ci chiediamo quali sono le curve più semplici che possiamo disegnare su un piano, la risposta sarà probabilmente, nell'ordine: 1) la retta, 2) la circonferenza. Queste curve, con cui siamo familiari, delimitano la maggior parte degli oggetti che ci circondano e le loro proprietà sono analizzate nei primi libri degli Elementi di Euclide. La geometria euclidea, descrivendo il mondo naturale in modo efficace e diretto, ha dominato per circa due millenni la scena matematica.
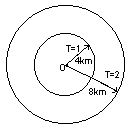 Se l'ecologo deve raggiungere un punto P, il percorso più breve è il segmento che unisce O con P. La geometria di questa foresta é nota come geometria euclidea. §2 LA CIRCONFERENZA DEL CICLISTA Dopo un anno la situazione cambia; dal nostro punto di vista cambia la geometria della regione. Viene infatti costruita una strada rettilinea che passa proprio dalla casa e l'ecologo si procura una bicicletta con la quale può muoversi a velocità v1 lungo la strada ed a velocità v2 nella foresta. Naturalmente abbiamo v2 £ v1 I nostri quesiti iniziali sono adesso più complessi e conviene riformularli:
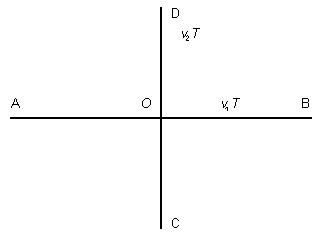 Naturalmente per raggiungere altri punti della foresta dobbiamo prendere in considerazione dei tragitti intermedi. Possiamo usare la strada per un tempo t1 e poi entrare nella foresta per il tempo rimanente T - t1. In questo caso i punti raggiungibili sono indicati in figura (ci limitiamo per simmetria al semipiano a destra dell'asse delle ordinate):
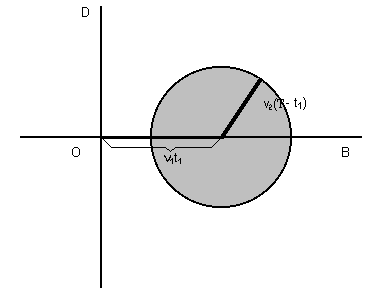 Unendo tutte queste regioni al variare di t1 da O a T otteniamo la regione cercata, il cui bordo verrà chiamato circonferenza del ciclista. Per determinare l'unione disegniamo la circonferenza con centro in O e raggio v2T e tracciamo le tangenti da B che ha coordinate (v1T, O). Le circonferenze Ct1 di raggio v2(T - t1) della figura precedente hanno centro che dista da B esattamente v1T - v1t1 = v1(T - t1). Tracciando dal centro di Ct1 la perpendicolare alla tangente QB troviamo un triangolo simile a OQB il cui lato parallelo a OQ é lungo (per similitudine) ancora Quindi la tangente QB é tangente anche a tutte le circonferenze Ct e si chiama il loro inviluppo. 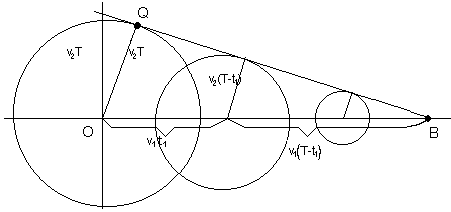 Per raggiungere un punto Z come nella figura seguente è disegnato il percorso. Notiamo che 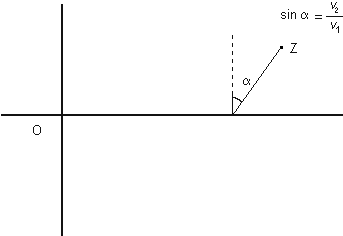 Possiamo disegnare infine la circonferenza del ciclista relativa al tempo T 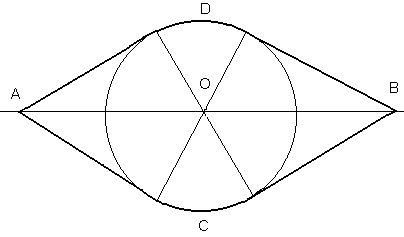 La retta ottenuta prolungando BZ ha equazione cartesiana La risposta che abbiamo ottenuto al primo quesito ci aiuta adesso a rispondere al Secondo quesito:L 'ecologo ciclista deve raggiungere parendo da O un punto P0 = (x0,y0). Qual è il percorso più breve (che chiameremo geodetica)? Otteniamo la risposta considerando la famiglia di tutte le circonferenze del ciclista centrate in O al variare di T. 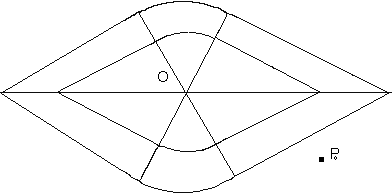 Dobbiamo cercare il valore di T minimo che comprende P0 all'interno della circonferenza corrispondente. Si presentano quindi due casi:
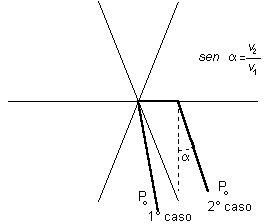 Allora la geodetica si ottiene come in figura tracciando da P0 la retta che incontra la verticale con angolo a con sin a =v2/v1 Parentesi analitica (può essere omessa da chi non conosce le derivate) Accenniamo alla soluzione analitica del secondo quesito (problema di minimo). Da questa soluzione è possibile, ma in modo meno diretto, risalire anche alla soluzione del secondo quesito (cioè alla circonferenza del ciclista). Il tempo impiegato per il percorso da O a P0 (nel primo quadrante) rimanendo nella strada per una lunghezza z è pari alla funzione Calcolando la derivata prima e ponendola uguale a zero si trova che è accettabile soltanto quando questo valore è non negativo. Infatti equivale con facili calcoli a che è l'equazione dell'angolo del punto 1) considerato in precedenza. §3 ANCORA SULLE GEODETICHE Abbiamo visto che la costruzione della strada porta il nostro ecologo a studiare un po' di matematica. Ben presto si rende però conto che non ha risolto tutti i suoi problemi perché non tutti i suoi spostamenti iniziano dalla casa. Ad esempio capisce subito che per spostarsi da due punti A e B lontani tra loro ma vicini alla strada
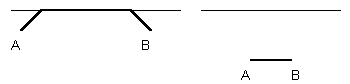 è conveniente raggiungere la strada mentre per due punti vicini tra loro ma lontani dalla strada la linea retta è sempre il percorso più breve. Cercando quindi un criterio che gli suggerisca in quali casi sia meglio servirsi della strada si pone il Terzo quesito: Qual è il percorso più breve (geodetica) che unisce due punti qualunque A e B della foresta? Per semplicità risponderemo a questo quesito solo nel caso in cui i due punti si trovano ad uguale distanza dalla strada (come avviene in entrambi i casi descritti nelle figure precedenti). In questo caso conviene considerare il punto M in cui l'asse di AB incontra la strada. Per la simmetria del problema, se il percorso minimo passa dalla strada, deve senz'altro passare anche da M. Verifichiamo quindi se il percorso minimo da A ad M (già risolto nel §2 pensando alla casa in M !) è più breve della metà del percorso rettilineo BA. In un sistema di coordinate centrato in M le coordinate di B ed A sono rispettivamente (xB, yB) e (-xB, yB). Posto a tale che sin a = v2/v1, la verifica richiesta equivale a Moltiplicando per v2 otteniamo x>B (sin a -1)+ yB cos a £ 0 Questa disuguaglianza è soddisfatta se ( xB, yB ) appartiene alla regione contenente l'asse delle ascisse e limitata dalle rette Queste due rette possono essere anche scritte come Il che mostra che quando v1 = v2 si identificano entrambe con l'asse delle ascisse. Pertanto per trovare la geodetica tra A e B (supposti al di sotto della strada) non dobbiamo fare altro che tracciare le due rette per M con coefficiente angolare ±Ö[(v1 - v2) / (v1 + v2)] La risposta è la seguente: se A e B sono interni alla regione determinata dalle due rette allora la geodetica coincide con il segmento che unisce A e B, altrimenti la geodetica passa da M ed è rappresentata in figura 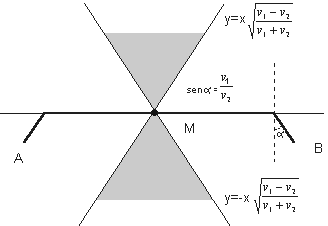 Per descrivere la geometria della regione introduciamo adesso un punto di vista completamente nuovo. Definiamo la distanza tra due punti come il tempo minimo che impieghiamo per andare dall'uno all'altro e corrispondentemente definiamo la lunghezza di una curva come il tempo impiegato a percorrerla. Con questo punto di vista (abbiamo cambiato la misura delle lunghezze!) le geodetiche sono le curve più corte tra quelle che uniscono due punti. Ad esempio abbiamo 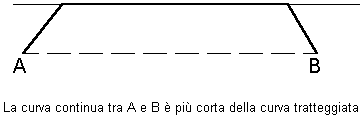 Adesso il nome "circonferenza" del ciclista assume pieno significato perchè essa viene vista come luogo dei punti equidistanti da un punto dato, esattamente come avviene per la circonferenza euclidea (vedi §1). Non sappiamo se il ciclista sia arrivato a questa conclusione, ma questo punto di vista si è fatto strada faticosamente nella storia della scienza, e può essere ricondotto essenzialmente alla nascita delle geometrie non euclidee, avvenuta intorno al 1830 per l'opera (indipendente) di J. Bolyay e N.I Lobacevskij. Essi riconobbero che sostituendo alla parola "retta" la parola "geodetica" era possibile ripetere gran parte degli Elementi di Euclide. Dalla lettura delle lettere private di K.F. Gauss risulta che egli aveva sviluppato un punto di vista analogo 20 anni prima ma non osò mai renderlo pubblico perchè temeva "le strida dei beoti". Più avanti accenneremo alle implicazioni logiche e filosofiche che rendevano prudente Gauss tanto da fargli scrivere questa famosa espressione. Può fare comunque riflettere che due secoli dopo il processo a Galileo da parte dell'Inquisizione, la libertà di pensiero nelle opinioni scientifiche era tutt'altro che acquisita. §4 UNA PARENTESI SULL'OTTICA GEOMETRICA Ci proponiamo ora di studiare quali sono i percorsi minimi in un piano che è diviso in due parti da una retta. In un semipiano ci si può muovere a velocità v1 mentre nell'altro la velocità è v2. Siano A e B due punti posti nei due semipiani diversi.
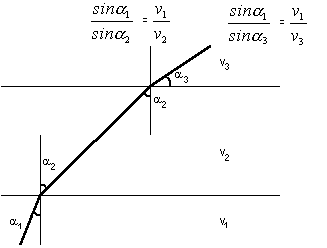
Nel caso che i due mezzi siano aria e acqua si ha v1 / v2 = 0.75, nel caso di aria e vetro si ha v1 / v2 = 0.66. La legge di rifrazione descrive quali sono le geodetiche nella regione precedente dove ancora una volta definiamo la distanza tra due punti come il tempo minimo necessario per passare da uno all'altro. Quando v1 = v2 allora la legge di rifrazione implica che a1 = a2 e quindi le geodetiche sono sempre segmenti di rette. La seguente figura illustra alcune geodetiche da A a B per diversi valori di v1 e v2. 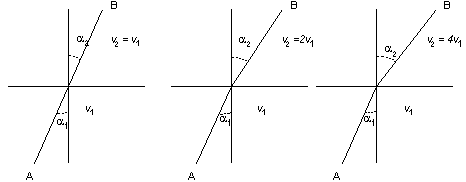 La seguente figura illustra alcune geodetiche con lo stesso angolo di incidenza a1 per diversi valori di v1 e v2. 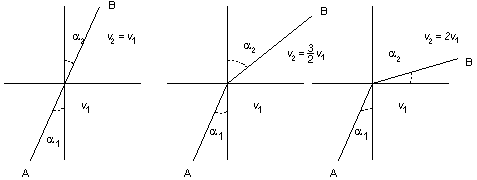 Dimostrazione della legge di rifrazione a1 e a2 sono legati dalla relazione che vediamo come una relazione implicita a2 = a2 (a1). La funzione tempo da minimizzare è da cui ponendo dt/da1 = 0 abbiamo Derivando (*) rispetto ad a1 otteniamo Sostituendo (***) in (**) si ricava che semplificando è proprio la legge di rifrazione. Quando l'angolo di incidenza a1 soddisfa a si ricava dalla legge di rifrazione che a2 è un angolo retto, e quindi il raggio luminoso non attraversa il secondo mezzo. Si parla allora di "riflessione totale". Questo è proprio il valore dell'angolo che avevamo trovato nel §2 a proposito del percorso minimo del ciclista. §5 DAL DISCRETO AL CONTINUO: UN MODELLO DI GEOMETRIA NON EUCLIDEA Il problema della rifrazione in due mezzi differenti si generalizza al caso in cui abbiamo tre mezzi (ad esempio in successione: aria, acqua, vetro). Il disegno seguente mostra che una geodetica è determinata adesso da 3 angoli a1 a2 a3 che soddisfano alle relazioni
 Dovrebbe adesso essere semplice immaginare una situazione in cui abbiamo molti mezzi differenti, disposti a strisce parallele come in figura, dove è mostrata una geodetica, che consiste in tanti piccoli segmenti di cui ciascuno incontra il successivo con angoli in rapporto predeterminato dalle velocità in ciascun mezzo. 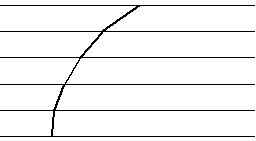 Se il lettore preferisce può immaginare il ciclista ecologo in una foresta fatta di tante strisce in ognuna delle quali può tenere una velocità diversa. Lo sforzo da compiere adesso è quello di passare dalla situazione "discreta" precedente ad una situazione "continua", dove la velocità non varia bruscamente da una striscia ad un'altra ma subisce dei mutamenti graduali in modo continuo. Possiamo immaginare un "passaggio al limite" dal discreto al continuo considerando delle strisce sempre più numerose e sempre più sottili. Nella situazione continua la velocità è una funzione positiva e continua (o meglio differenziabile) f(y) dipendente solo dalla ordinata y. Nel piano euclideo f è una funzione costante (che possiamo supporre uguale ad 1 in opportune unità di misura) La relazione tra il discreto e continuo è una delle problematiche più antiche del pensiero umano, ed è presente in numerosi scritti di Aristotele, Democrito, Zenone e altri pensatori greci. Si veda [J.L.Manin, voce "Continuo/discreto" in Enciclopedia , Einaudi 1978]. il calcolo differenziale introdotto da Newton e Leibniz ha fornito uno strumento formidabile per trattare i fenomeni continui ed ha trovato uno dei più grandi successi con la relatività generale di Einstein, che permette di descrivere il mondo fisico in grande scala. D'altronde la meccanica quantistica introduce un modo di pensare "discreto" nei fenomeni relativi alle particelle elementari (in piccola scala) e non è stata ancora trovata una teoria soddisfacente che unifichi queste due visioni. Nel campo della biologia la scoperta del DNA ha mostrato come i mattoni su cui si fonda la vita sono discreti. Negli ultimi anni la matematica discreta ha avuto un forte impulso per la diffusione del computer, il cui funzionamento è basato su fenomeni discreti. È difficile stabilire se il modello discreto con numerose e sottili strisce sia più aderente alla realtà del modello continuo con la funzione velocità f(y). Per i nostri scopi dobbiamo solo pensarli come due modelli matematici differenti. Il modello continuo ci permetterà di trovare delle soluzioni molto semplici ed eleganti. Per determinare le geodetiche nel modello di piano dove la velocità è una funzione f(y) della distanza y da una retta fissata (asse delle ascisse) consideriamo nuovamente il caso con N strisce differenti. Nella figura seguente è mostrata una geodetica che incontra con angolo a (y) l'asse verticale all'altezza y. Consideriamo dei punti di ordinata y1, y2, ...,yN ciascuno in una striscia differente. Nella striscia che contiene yk l'angolo con la verticale è a(yk) e la velocità è f(yk). 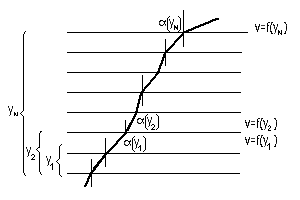 La legge di rifrazione ci dice allora che per k=1,2,...,N-1. Questa equazione ha senso quando l'angolo di incidenza non è nullo, cioè quando la direzione non è verticale. In questo caso è evidente che le rette verticali rappresentano sempre percorsi minimi tra due punti. L'equazione precedente si può scrivere come sin(a (yk+1 )) / f (yk+1) = sin(a (yk ) / f(yk) e questa scrittura mostra che sin (a(y)]/f(y) è indipendente da y!! Questo è vero qualunque sia il numero delle strisce, pertanto ricaviamo che nel modello continuo dove K è una costante. Una cosa salta subito agli occhi: nel caso in cui f(y) = y (questo è il caso più semplice dopo il caso euclideo) il rapporto K = sin(a(y)) / f(y) = sin(a(y))/y rappresenta la lunghezza del raggio perpendicolare alla traiettoria che unisce il punto di altezza y con l'asse delle ascisse: 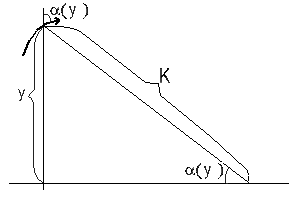 Il fatto che questo raggio sia costante ci dice quindi che il punto si muove su una circonferenza di raggio K con centro sull'asse delle ascisse. Diamo un nome al semipiano superiore {y > 0} dove i punti si muovono in ogni direzione con velocità f(y) = y, che si dice piano iperbolico (o semipiano di Poincaré). Abbiamo ricavato il Teorema Le geodetiche del piano iperbolico sono le semirette verticali e le semicirconferenze con centro sull'asse delle ascisse. L'interpretazione fisica del risultato precedente è la seguente: in un vetro in cui la velocità della luce (=indice di diffrazione) varia in modo lineare con la distanza da un bordo rettilineo, un raggio laser descrive traiettorie date da semicirconferenze o da rette. Notiamo adesso il seguente risultato (il lettore provi a sostituire "iperbolico" con "euclideo" e "geodetica" con "retta"...): Per due punti qualunque del piano iperbolico passa una ed una sola geodetica. Dimostrazione se la retta che unisce i due punti A e B è verticale è anche una geodetica. Se non è verticale allora l'asse del segmento AB incontra l'asse delle ascisse in un punto C che è centro di una semicirconferenza (geodetica) passante da A e B. C è l'unico punto sull'asse delle ascisse equidistante da A e B (proprietà dell'asse di un segmento) e quindi la semicirconferenza trovata è unica. Uno dei postulati della geometria euclidea è il celebre Postulato delle parallele che recita: Per un punto P del piano euclideo esterno ad una retta r passa una unica retta che non incontra r (parallela ad r). Adesso sostituendo "euclideo" con "iperbolico" e "retta" con "geodetica" l'enunciato precedente diventa falso! Il disegno seguente mostra infatti infinite geodetiche per P che non incontrano la geodetica r 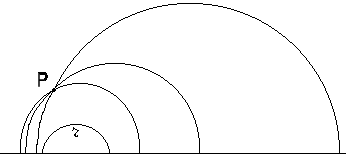 Questo fatto ha una fortissima importanza storica. Il Postulato delle parallele è meno intuitivo rispetto agli altri postulati (ad esempio rispetto al postulato sulla unicità della retta per due punti). Pensando che la geometria euclidea avesse un valore "assoluto" per due millenni numerosi matematici (prima di Bolyay e Lobacevskij) hanno tentato di dimostrare (si veda [Meschkowsky]) il postulato delle parallele a partire dagli altri postulati della geometria euclidea. Siccome gli altri postulati sono tutti verificati nel piano iperbolico (con la sola accortezza di sostituire "retta" con "geodetica"), se una tale dimostrazione esistesse si dovrebbe applicare anche al piano iperbolico. Ma nel piano iperbolico il postulato delle parallele è falso e quindi una dimostrazione non può esistere. Si noti la sottigliezza logica di dimostrare "l'impossibilità di avere una dimostrazione". Questo significa che il postulato delle parallele va effettivamente aggiunto agli altri assiomi ed è proprio quello che rende euclidea la geometria , facendole perdere ogni carattere "assoluto". La geometria euclidea è considerata oggi come una delle tante geometrie. Seguitando l'analogia con l'esempio del raggio laser osserviamo che un vetro con indice di diffrazione costante è uno dei tanti vetri che si possono costruire. Riprenderemo alla fine del §6 il calcolo delle geodetiche per un piano dove la funzione velocità f(y) è qualunque. §6 CIRCONFERENZE IPERBOLICHE E CURVATURA GAUSSIANA Ci proponiamo adesso di descrivere la lunghezza (non euclidea) di una curva nel piano dove la velocità è data da f(y) funzione della distanza y dalla retta delle ascisse. La seguente motivazione può essere omessa da chi conosce già gli integrali.
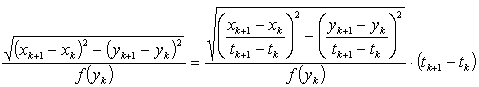 Sommando per k=l,2,...,N e passando al limite per N® ¥ si trova il seguente Lemma Data una curva di equazioni parametriche x = x(t), y = y(t) per a £ t £ b nel piano, un punto che la percorre con velocità f(y(t)] impiega un tempo pari a 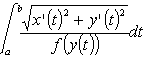 Siamo ora pronti per una definizione "rivoluzionaria": Definizione Data una curva C di equazioni parametriche x = x(t), y = y(t) per a £ t £ b nel piano non euclideo descritto da una funzione positiva "velocità" f(y), la sua lunghezza L(C) è 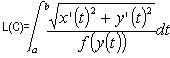 (*) (*)Nel linguaggio di Riemann ds2 = (dx2 + dy2)/f2(y) si dice il tensore metrico e la formula precedente si può leggere come L:= òds. Come caso particolare abbiamo la lunghezza delle curve nel piano iperbolico. Definizione Data una curva di equazioni parametriche x = x(t), y = y(t) per a £ t £ b nel piano iperbolico, la sua lunghezza è 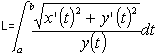 Una varietà riemanniana è grossomodo uno spazio dove è definita una nozione di lunghezza per le curve. Il piano non euclideo con una funzione "velocità" f(y) è una varietà riemanniana. In questo ambito una geodetica è definita (grossomodo) come una curva che è il percorso più corto tra due qualunque suoi punti. Un esempio più familiare di varietà riemanniana è la sfera, dove le geodetiche sono date dalle circonferenze ottenute tagliando la sfera con piani passanti per il suo centro. Le rotte aeree seguono approssimativamente le geodetiche sulla Terra. Le geodetiche nel piano dove le lunghezze sono descritte dalla (*) tagliano la verticale con un angolo a(y) che soddisfa con K costante. Quindi abbiamo 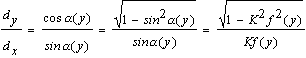 da cui si ricava la formula per un arco di geodetica espresso come x=x(y) dove C è un'altra costante. Quando f(y)=y la soluzione dell'integrale precedente è che è infatti l'equazione di una arco di circonferenza di centro (C,0) e raggio K. Nel caso del piano iperbolico la distanza tra due punti (detta distanza iperbolica) si può calcolare risolvendo l'integrale che determina la lunghezza della geodetica tra i due punti. E' facile verificare che la distanza tra i due punti con la stessa ascissa (x,y1) e (x,y2) è data da Nel caso in cui i due punti P1 e P2 sono come in figura 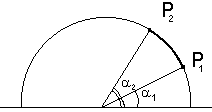 si può verificare (con tecniche standard in ogni corso universitario di Analisi I) che la distanza è data da Non avremo più bisogno di questo ultimo risultato. Nel caso del piano iperbolico diamo adesso la costruzione delle circonferenze. Per fare questo abbiamo bisogno di una parentesi, interessante di per sé. Consideriamo una circonferenza C di centro O e raggio R nel piano. L'inversione rispetto a C è una trasformazione del piano che porta tutti i punti esterni a C in punti interni e viceversa. I punti di C rimangono invariati. Precisamente l'immagine Posto P = (x, y), 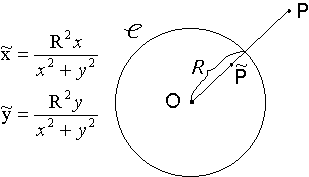 Il lettore può facilmente verificare che applicando ancora l'inversione all'immagine di un punto P si ritrova il punto P di partenza. Se (x(t), y(t)] sono le equazioni parametriche di una curva, l'immagine della curva attraverso l'inversione è data da 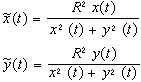 Lemma Con le notazioni precedenti, vale per ogni valore del parametro t Dimostrazione. Si calcola 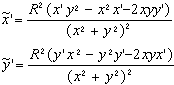 da cui dopo qualche calcolo e quindi 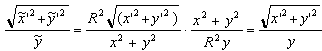 Corollario Le lunghezze nel piano iperbolico di una curva e della sua immagine attraverso una inversione rispetto ad una circonferenza con centro sull'asse delle ascisse sono le stesse. Dimostrazione Con una traslazione orizzontale si può supporre che la circonferenza abbia centro nell'origine. La tesi segue allora dal lemma precedente e dalla definizione di lunghezza. La proprietà del corollario precedente si riassume affermando che l'inversione rispetto ad una circonferenza è una isometria del piano iperbolico, così come le traslazioni e le rotazioni sono isometrie del piano euclideo. Lemma Sia C una circonferenza di centro O e raggio R. Sia P un punto esterno. Siano A e B i punti di tangenza delle tangenti condotte da P a C. Allora la circonferenza C' centrata in P e passante per A e B (che è ortogonale a C) è trasformata in se stessa dall'inversione rispetto a C. Dimostrazione Sia Q Î C' e sia Q' l'altra intersezione della retta OQ con C'. Il teorema della secante e della tangente implica che 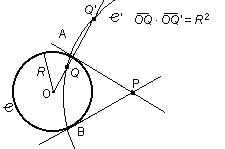 il che implica che Q' è l'immagine di Q attraverso l'inversione. Teorema (LE CIRCONFERENZE NEL PIANO IPERBOLICO) Il luogo dei punti che hanno distanza iperbolica R dal punto P = (x, y) è una circonferenza euclidea C con centro in (x, y cosh R) e raggio y sinh R. Dimostrazione I punti sulla verticale di P che hanno distanza iperbolica pari a R sono i due punti P1 = (x, y1)e P2 = (x, y2) che soddisfano alle equazioni da cui Il punto medio tra i due punti è quindi (x, y cosh R) e la circonferenza centrata in questo punto passante per i due punti ha raggio y sinh R ed è proprio la C cercata. Dobbiamo provare che tutti gli altri punti di C hanno distanza iperbolica R da P. 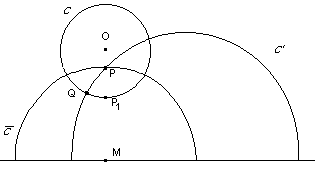 La circonferenza (verificabile anche per via analitica). Sia C' un'altra qualunque circonferenza per P (e S) con centro sull'asse delle ascisse che incontra C in Q. Abbiamo (OQ)2 = OP . OS da cui per il teorema della secante e della tangente C' è ortogonale a C. Per il lemma precedente l'inversione rispetto a C' porta C in se stessa e lascia invariato P. Quindi Q viene portato dall'inversione in un altro punto di C che ha ancora distanza R da P. Siccome Q è qualunque segue la tesi. Si può calcolare (sempre con tecniche standard in ogni corso di Analisi I) la lunghezza della circonferenza iperbolica di cui al teorema precedente. Il risultato del calcolo(che omettiamo) è ed un fatto importante è che è indipendente dal punto !! Per piccoli valori di R l'espressione precedente può essere approssimata con dove i termini successivi corrispondono a potenze in R di ordine superiore a 3 e che sono trascurabili per R piccolo. Notiamo che il primo termine corrisponde al valore euclideo mentre i termini successivi portano delle "correzioni". In generale la circonferenza geodetica di raggio R nel piano con metrica indotta dalla "velocità" f(y) ha la lunghezza (per R piccolo): dove ancora i termini successivi contenenti potenze di R di ordine superiore a 3 e quindi trascurabili. (Questo risultato richiede l'introduzione delle "coordinate geodetiche" ed è più avanzato).La quantità si dice curvatura gaussiana e descrive il primo termine correttivo da apportare alla lunghezza della circonferenza rispetto al valore euclideo. -Nel piano euclideo abbiamo e quindi K = 0. -Nel piano iperbolico abbiamo e quindi K = -1. Gli analoghi dei triangoli euclidei sono rappresentati dai triangoli geodetici , cioè da regioni di piano limitate da tre archi di geodetica. Il seguente disegno descrive un triangolo geodetico nel piano iperbolico 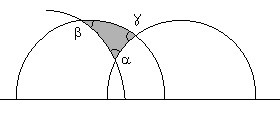 Nel piano euclideo la somma degli angoli interni ad un triangolo è pari a p radianti (corrispondenti a 180° gradi). Questo enunciato è equivalente al Postulato delle parallele. È interessante osservare che nel piano iperbolico la somma degli angoli interni è sempre minore di p. Invece sulla sfera un triangolo geodetico ha somma degli angoli interni sempre maggiore di p. Il tensore metrico permette anche di calcolare le aree di regioni del piano, con un procedimento di calcolo integrale che omettiamo. Non possiamo però omettere un bellissimo risultato di Gauss, secondo cui nel piano iperbolico l'area di un triangolo geodetico con angoli pari a a, b, g è uguale a Notiamo che il fatto che l'area sia positiva porta alla disuguaglianza che abbiamo appena menzionato. Inoltre il fatto che l'area del triangolo dipende solo dagli angoli è caratteristico del caso in cui la curvatura gaussiana è costante ma non nulla. Il concetto di curvatura è stato generalizzato da Riemann a spazi con un numero qualunque di dimensioni. Come abbiamo accennato, l'applicazione più importante di questi concetti matematici è senz'altro la relatività generale di Einstein, che nel 1979 ha ricevuto una ulteriore verifica sperimentale dall'osservazione di lontane galassie (fenomeno della "lente gravitazionale"). Il nostro ecologo termina così il suo viaggio, probabilmente un po' confuso da tante idee che non si aspettava. Speriamo che gli appunti di questo viaggio gli siano da stimolo verso studi più approfonditi.
Euclide di Alessandria pubblicò gli "Elementi" intorno al 300 a. C. Gli Elementi di Euclide sono uno dei primi manuali di geometria piana e spaziale che procedono per via deduttiva da alcuni postulati. La prima edizione a stampa degli Elementi uscì a Venezia nel 1482 e da allora in poi ne sono state pubblicate almeno un migliaio di edizioni. Gli Elementi sono stati usati come libro di testo in quasi tutti i ginnasi fino al secolo scorso.
Dopo pochi minuti scrisse quindi il risultato esatto 5050 sulla lavagnetta lasciando allibito l'insegnante. A 21anni ricevette il dottorato dando una dimostrazione del "teorema fondamentale dell'algebra", avendo l'idea di rappresentare i numeri complessi come punti del piano. I contributi di Gauss spaziano dalla teoria dei numeri all'astronomia, dall'analisi matematica alla statistica. La distribuzione "a campana" che si verifica nella maggior parte dei fenomeni naturali è chiamata in suo onore gaussiana. Gauss lavorò quasi tutta la vita presso la città tedesca di Göttingen, della quale diresse l'Osservatorio Astronomico. Celebre è il calcolo compiuto da Gauss dell'orbita del pianetino Cerere. Sulla base di poche osservazioni compiute nel 1801, egli fu in grado di predire il ritorno del pianetino con un anno di anticipo, applicando il metodo dei minimi quadrati. Nel 1816 Gauss ricevette l'incarico di dirigere le misurazioni geodetiche del regno di Hannover. Durante le misurazioni calcolò la somma degli angoli interni di un enorme triangolo con vertici tre cime montuose, cercando qualche scostamento dal valore aspettato di 180° (si veda il §6 di queste note). Il valore ottenuto non si discostò da 180° più degli errori sperimentali, lasciando aperta la verifica del grado di applicabilità della geometria euclidea.
Un'esposizione dettagliata della geometria iperbolica, insieme a molte notizie storiche sul postulato delle parallele si può trovare nel classico
|