Mauro Cerasoli, mauro.cerasoli@alice.it Università di L'Aquila 1. Premessa Fin dall'antichità l'aritmetica e la geometria sono state ritenute le due anime della matematica. Colonne d'Ercole di questo pregiudizio furono, e rimangono, le celebri frasi "il numero governa l'universo" di Pitagora e "vietato l'ingresso a chi non è geometra" di Platone. Lo stesso Galilei ripeteva, circa venti secoli dopo, "l'universo è scritto in linguaggio matematico e i caratteri sono i triangoli, cerchi ed altre figure geometriche". La geometria analitica di Cartesio sposava queste due anime e poi, con Leibniz e Newton, si aggiungeva la terza colonna: l'analisi. Abbellita dalla topologia, quest'altra faccia della matematica assumeva il ruolo di prima donna soprattutto a livello accademico, nel senso di numero di cattedre messe a concorso. Un'altra faccia importante della matematica, la teoria della probabilità, o più semplicemente, la probabilità, è stata invece un po' trascurata. Infatti sarebbe sparita dai corridoi dei dipartimenti matematici se non fossero state aperte le Facoltà di Scienze Statistiche o se i fisici non avessero scoperto che nel microcosmo le idee di Galilei e Newton vanno a farsi friggere. A riprova, il fisico e grande divulgatore della matematica, Simon Singh, autore del bestseller L'ultimo teorema di Fermat e del più recente Codici & Segreti, intervistato dal Corriere della Sera il 24 luglio '99, sul tema L'invenzione del Millennio, rispondeva: " la teoria dei quanti le va bene?" E la teoria dei quanti non si basa sul concetto di probabilità, concetto che Maxwell nel 1854 riteneva a base della vera logica di questo mondo? Scopo di questo lavoro è far vedere con esempi concreti, che esiste una interpretazione probabilistica di concetti di algebra (e di analisi, quindi, per transitività, di geometria) così come esiste quella geometrica. Per esempio, se scrivo x2 dico "ics al quadrato" pensando, geometricamente, al quadrato di lato lungo x. Così per x3, penso ad un cubo di lato lungo x. Infatti a conferma di questo modo di pensare, di intendere, una nota serie numerica prende l'attributo di geometrica per tale motivo. Più giusto sarebbe stato chiamarla serie combinatoria visto che x4, x5 ecc. non hanno alcun significato geometrico reale. Invece per ogni coppia di naturali x ed n, la potenza xn è il numero di disposizioni (con ripetizione) di x oggetti ad n ad n. Così 313 è il numero di colonne possibili al totocalcio. E il calcolo combinatorio è stato l'anticamera del calcolo delle probabilità. In generale il significato geometrico di una espressione algebrica (o analitica) o di un concetto algebrico (o analitico) si fonda partendo dal piano (o spazio) cartesiano R2. Così ad un numero reale corrisponde un punto sulla retta (e viceversa), ad una equazione del tipo ax + by + c = 0 corrisponde una retta (e viceversa). Al punto medio del segmento di estremi a e b corrisponde l'ascissa (a + b)/2 ecc.: fatti ben noti ad un laureato in matematica. Per illustrare il significato probabilistico riteniamo noti i concetti di fenomeno casuale (o prova, o esperimento), evento, probabilità, variabile aleatoria, media (o speranza matematica). 2 - Richiami sulle variabili aleatorie. Per comodità del lettore ricordiamo che una v.a. X semplice (o finita) è una coppia (vk ; pk) k = 0, 1, 2, ... , n, dove vk sono numeri reali arbitrari (detti valori possibili per X) e pk = P(X = vk) è la probabilità che X prenda il valore vk tale che La v.a. X è detta discreta se k ÎN = { 0, 1, 2, ... } e naturale se vk = k per ogni k Î N. Esempi 1. La moneta B = (0, 1 ; 1-p, p) 0 < p < 1 di trucco p (o v.a. di Bernoulli) prende il valore 0 con p. 1 - p ed il valore 1 con p. p. Nel lancio di una moneta testa - croce essa risponde alla domanda: quante teste escono? B si dice equa (o simmetrica) se p = ½. 2. Il dado s - dimensionale (o simmetrico, o salomonico) D(s) = (1, 2, 3, ... , s ; 1/s)s = 2, 3, ... prende i valori 1, 2, 3, ... , s con la stessa p. 1/s. Casi particolari: a) s = 2, moneta equa di Bernoulli D(2) = B+1; b) s = 4, tetraedro regolare D(4); c) s = 6, dado comune D(6); d) s = 37, roulette; e) s = 90, estrazione di un numero al lotto. 3. La cifra in base s è la v. a. C(s) = D(s) - 1 = (0, 1, 2, .. , s - 1; 1/s) In particolare C(2) è la cifra binaria o v.a. di Bernoulli B equa e C(10) è la cifra decimale C = (0, 1, 2, 3, ... , 8, 9 ; 1/10). C(s) corrisponde all'estrazione casuale di una cifra in base s. Per s = 10 l'estrazione a caso può essere fatta con a)un mazzo di carte napoletane: asso = 1, due = 2, ecc., il fante = 8, il cavallo = 9, il re = 0; b)l'estrazione del Lotto: in una ruota (città) fissata, la cifra estratta è il resto della divisione per 10 del primo numero estratto; c)computer o calcolatrice, ad esempio TI-89, mediante il tasto rand. 4. Fissato un naturale m, la v. a. D(s º m), uguale a D(s) modulo m, detta s - dado modulo m, prende i valori uguali al resto della divisione di s per m. Ad esempio D(3 º 3) = (0, 1, 2; 1/3) D(4 º 3) = (0, 1, 2; ¼, ½, ¼) D(5 º 3) = (0, 1, 2; 1/5, 2/5, 2/5) 5. La v. a. geometrica T1 è il tempo d'attesa, ovvero il numero di lanci di una moneta di Bernoulli necessari per avere la prima testa: vn = n; pn = p(1 ... p)n - 1 n = 1, 2, 3. 6. La v. a. di Poisson Na(t ) è il numero di arrivi (eventi rari) nell'intervallo di tempo (o spazio) t quando a è l'intensità media di arrivi: vk = k; pk = (at)ke-at/k! , k = 1, 2, 3, ... Le v. a. X ed Y sono equidistribuite (o somiglianti) se assumono gli stessi valori con le medesime p., cioè se P(X= k) = P(Y = k) per ogni loro valore k. In altri termini, l'una è copia o ripetizione (una clonazione) dell'altra. X e Y sono indipendenti se per ogni coppia di valori possibili i e j risulta P(X = i ; Y = j) = P(X = i)P(Y = j) dove ; sta per "et" . Questo concetto di indipendenza si estende a più di due v. a. 3. Il significato probabilistico Il significato probabilistico può essere cercato tenendo presente quanto segue:
Ciò può sembrare vago ed impreciso ma una bella sfilza di esempi concreti dovrebbe dare un'idea più chiara della questione (almeno si spera) Esempio. Un numero reale di [0, 1] Sia x un numero di [0, 1] scritto in base 10 nella forma Consideriamo la successione di v. a. Cn = Cn(10), n = 1, 2, 3, ... . (vedi esempio 2.3) Cn(10) = (0, 1, 2, ... , 8, 9 ; 1/10) indipendenti per ipotesi. La v. a. R = C110-1 + C210-2+ ... + Cn10-n + ... è un numero reale estratto a caso in [0, 1] (R sta per random). Consideriamo l'evento (R < x) = "il numero R estratto a caso è minore di x". La sua p. si può calcolare subito: 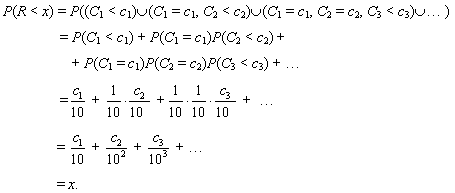 Quindi un x Î [0,1] è la p. di scegliere un punto a sinistra di x nel tiro a segno a caso in [0, 1]. L'evento (R < x) è "il punto scelto a caso cade in [0, x[". Se invece di un punto R scegliamo a caso in [0, 1] due punti R1 e R2 indipendenti, fissati x1, x2 Î [0, 1], l'evento (R1 < x1, R2 < x2) = "il punto (R1, R2) estratto in [0, 1]2 appartiene al rettangolo [0, x1[ ´ [0, x2[" ha p. x1x2. 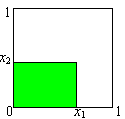 fig. 2 fig. 2Analogo discorso per il prodotto x1x2x3 di tre o più numeri x1, x2 e x3 di [0, 1]. Allora x2 è la p. che un punto scelto a caso nel quadrato unitario [0, 1]2 cada nel quadrato [0, x]2 (fig. 2). Così x3 è la p. che un punto scelto a caso nel cubo unitario [0, 1]3 cada nel cubo [0, x]3 ecc. con analogo significato probabilistico per il monomio xn: è la p. che scelti n punti a caso in [0, 1] tutti cadano a sinistra di x. Al contrario, 1 - xn è la p. che almeno uno di essi cada a destra di x. Lasciamo come esercizio la spiegazione probabilistica della classica identità (cfr. M.Cerasoli, Esempi di dimostrazioni probabilistiche, Lettera Pristem, 29(1998)38-43): 4. Operazioni e funzioni simmetriche Le operazioni aritmetiche elementari più note sono l'addizione e la moltiplicazione. In termini geometrici la prima dà luogo al semiperimetro e la seconda all'area di un rettangolo. Dati x e y Î [0, 1], siano A e B due eventi incompatibili ed indipendenti tali che P(A) = x e P(B) = y. Allora, come è ben noto x + y = P(A È B), xy = P(A Ç B) ed abbiamo individuato così il significato probabilistico di queste due operazioni. C'è però un'altra operazione aritmetica che è molto importante nella teoria dell'affidabilità e meno nota delle due su viste. Nei circuiti 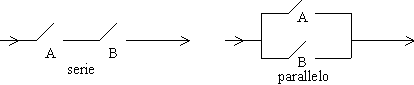 siano A e B due porte indipendenti con rispettive p. x ed y di funzionamento. L'affidabilità del circuito, cioè la p. che funzioni, è rispettivamente
Nel caso serie, nulla di nuovo: la solita moltiplicazione, ma nel caso parallelo abbiamo una nuova operazione tra numeri reali che non ha alcun riscontro geometrico. Se si hanno n porte indipendenti o sistemi in serie (o in parallelo), ciascuno di affidabilità x, l'affidabilità del circuito è
Tutte le porte funzionano nel primo caso, almeno una funziona nel secondo caso. Sempre nel caso parallelo, se le n porte hanno affidabilità rispettivamente x1, x2, ..., xn, l'affidabilità del sistema parallelo è
sono le funzioni simmetriche elementari nelle variabili x1, x2, ..., xn. 5. Combinazioni lineari Siano A1, A2, ..., An eventi incompatibili ed esaustivi, ovvero una partizione dell'evento certo. In termini concreti, uno solo di essi può verificarsi. Per ogni indice i sia ai = P(Ai). Sia poi bi, per i = 1, 2, ..., n, la p. che un evento B si verifichi una volta accaduto l'evento Ai. Allora la combinazione lineare a1 b1 + a2b2 + ... + anbn è la probabilità che si verifichi B. 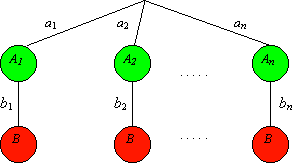 (fig. 1) (fig. 1)Una combinazione lineare può avere un altro significato probabilistico in termini di media (o speranza matematica) di una v. a.. Infatti, data la v. a. X = (v0, v1, ... , vn; p0, p1, ... , pn) la sua media <X> è definita come segue: < X > = v0p0 + v1p1 + ... + vn pn Con le opportune precisazioni tutto ciò si estende al caso in cui la v. a. X assume infiniti valori. Per gli esempi visti al §.2 la definizione è ancora valida con il solo avvertimento di aggiungere + ... e passare quindi ad una serie. E' utile ricordare che la media < X > di una v. a. X gode delle seguenti proprietà
Le v. a. degli esempi del §.2 hanno medie rispettive: 1. p; 2. (s + 1)/2; 5. 1/p; 6. at. 6. Polinomi e serie di potenze Sia N una v. a. che assume il valore k con p. pk per k = 0, 1, 2, ..., n. Interpretiamola come il lancio di un dado: se esce la faccia k, estraiamo k punti a caso dall'intervallo [0, 1]. Fissato x Î [0, 1] si vede subito che p0 + p1x + p2x2 + ... + pnxn (6, 1) è la p. che tutti i punti estratti cadano a sinistra di x. E' questo un primo esempio di processo stocastico randomizzato. Ad essere randomizzato è il numero di punti che vengono estratti. In altri termini, al numero n di punti estratti nel §.4 viene sostituita la v. a. N. Esempio. Se N è D(5 º 3) = ( 0, 1, 2; 1/5, 2/5, 2/5) allora la (6,1) diventa il trinomio Un altro significato probabilistico del polinomio (6, 1) è dato dal concetto di media di una v. a.: esso è la media della v. a. xN. Infatti < XN > = p0 + p1x + p2x2 + ... + pnxn. 7. Polinomi e funzioni generatrici I polinomi vengono utilizzati nella teoria della probabilità anche in una forma diversa dalla precedente (Laplace 1812). Il polinomio (6, 1) è inteso nella variabile reale x. Per un dato valore reale x e per assegnate probabilità pk , esso è un numero reale di [0, 1]. Ma esistono anche polinomi nella variabile formale (o indeterminata) t. In particolare, data una v. a. naturale X che prende il valore k con probabilità pk, k = 0, 1, 2, ... , n, il polinomio p0 + p1t + p2 t2 + ... + pn tn nella variabile formale t è detto polinomio generatore (p.g.) di X. Noi lo indicheremo con < X; t > per esprimere la dipendenza da X. Il significato probabilistico è il seguente: il coefficiente di tk è la probabilità che X prenda il valore k. Esempi
Più in generale, se X = (vn; pn) è una v. a. che prende il valore vn con probabilità pn, per n = 0, 1, 2, ... la funzione generatrice di X è la serie di potenze formale Esempi. 1. La v. a. geometrica T>1 ha funzione generatrice p / [1 - (1 - p) t]; 2. La funzione generatrice della variabile Na ( t ) di Poisson è e a t (t - 1); 3. Nel gioco del tresette con le carte napoletane, il valore di una carta è il seguente:
Pertanto la v. a. (0, 1/3, 1; 2/5, 1/2, 1/10) ha funzione generatrice
dove D è l'operatore derivata (Dtn = ntn - 1 esteso per linearità ai polinomi). 8. Il prodotto di polinomi L'antico gioco della zara (dall'arabo zahr, dado) consiste nel lanciare due o più dadi e puntare sulla somma dei punti usciti. Il gioco dei dadi X e Y fornisce quindi un primo esempio di somma X + Y di due v. a. semplici. Come si determina la distribuzione di X + Y, cioè la probabilità che X + Y prenda il valore k? Aquesta domanda risponde il seguente Teorema di convoluzione. Se X e Y sono v. a. indipendenti la funzione generatrice della somma X + Y è il prodotto delle funzioni generatrici di X e di Y: < X + Y ; t > = < X; t>< Y; t>. In particolare, se X1, X2, ... , X>n sono v. a. indipendenti ed equidistribuite la funzione generatrice della somma Sn = X1 + X2 + ... + Xn è < X1 ; t > n. Esempi 1. Problema di Galilei. Il polinomio generatore del lancio di tre dadi è (t + t2 + ... +t6)3/216. La probabilità che si faccia il punto k lanciando tre dadi è il coefficiente di tk nel polinomio precedente. Per la formula del caso più generale del lancio di n s- dadi si veda M. Cerasoli, Problemi risolti di Calcolo delle Probabilità, CEA,1991. 2. Si lanciano una moneta equa B di Bernoulli ed un dado equo D modulato (5 º 3). La p. che B + D sia uguale a k è il coefficiente di tk nel prodotto B + D = (0,1, 2, 3; 1/10, 3/10, 2/5, 1/5) Il teorema di convoluzione esprime il fatto seguente: se ak è il coefficiente di tk nel polinomio p(t) e bk è il coefficiente di tk in q(t), allora il coefficiente cn di tn nel prodotto p(t)q(t) è dato dalla somma di prodotti ak bn - k al variare di k da 0 ad n. Questa proprietà è valida in virtù del significato probabilistico di una combinazione lineare visto al §.6. Infatti se la somma dei punti X + Y deve essere uguale ad n, allora X può essere k ed Y deve essere n - k (p. ak bn - k) al variare di k da 0 ad n (somma su k). 9. La composizione di polinomi Si è visto che il prodotto di polinomi corrisponde al lancio di due o più dadi. Infatti siamo partiti dal problema del lancio di due dadi ed abbiamo scoperto che per risolverlo interviene il prodotto di polinomi. Questo modo di procedere ci fa tornare in mente, andando lontano nei ricordi del liceo, quei problemi di geometria analitica in cui si partiva da un concetto geometrico, per esempio retta, circonferenza, parabola ecc., già noto, e poi si approdava alla relativa equazione cartesiana. Dopo abbiamo invertito la questione e dai concetti algebrici o analitici siamo passati a figure geometriche. Ad esempio, nel cercare il grafico di funzioni o la curva di una data equazione cartesiana. In altri termini, partendo dal concetto algebrico si voleva ritrovare l'analogo concetto geometrico. Ma allora facciamo la stessa cosa per la probabilità. Ci domandiamo: se il prodotto di polinomi corrisponde al lancio di due dadi, cioè alla somma di due variabili aleatorie, a che cosa corrisponde la composizione di due polinomi? Ovvero, se x(t) ed y(t) sono i polinomi generatori delle variabili X e Y , esiste qualche fenomeno casuale interpretabile con le composizioni funzionali x(y(t)) e y(x(t)) ? Il polinomio x(y(t)) (e così pure y(x(t))) è generatore di qualche v.a.? Quale? Ovviamente la risposta è affermativa. Date le v.a. semplici X e Y si consideri il fenomeno casuale organizzato nel seguente modo:
Esempio Siano X un dado ed Y una moneta di Bernoulli; lancio il dado e, per ipotesi, esce il 4; ora lancio 4 volte la moneta. Se, sempre per ipotesi, escono 0, 1, 1 e 0, allora il risultato di questo nuovo fenomeno casuale (o processo stocastico) è 2: la somma dei punti usciti nei 4 lanci della moneta. In tal modo abbiamo definito una nuova v.a. mediante X e Y che indicheremo con XçY. Si noti che l'ordine dell'operazione è importante: YçX è diverso da XçY. Possiamo definire questa nuova v.a. anche ponendo XçY = Y1 + Y2 + ... + YX Dove le Yk sono v.a. indipendenti e somiglianti a Y. Infatti XçY è la somma aleatoria di X copie di Y. Se X è una v.a. certa che assume il valore n con p. 1, cioè se P(X=n)=1, allora XçY = nçY = Y1 + Y2 + ... + Yn Si riduce alla somma (deterministica) usuale di n copie di Y. Definita la v.a. XçY possiamo dare l'interpretazione probabilistica della composizione di polinomi. Teorema Siano x(t) e y(t) i polinomi generatori delle v.a.indipendenti X e Y; allora x(y(t)) è il polinomio generatore di XçY, ovvero P(XçY=k) = Dkx(y(t))/k!|t=0 Esempio Il polinomio generatore del dado usuale X è (t+t2+ ... +t6)/6 mentre quello della moneta equa Y è ½+t/2. Pertanto il polinomio generatore di XçY è [1/2+t/2+(1/2+t/2)2+ ... +(1/2+t/2)6]/6 = 21/128+5t/16+33t2/128+t3/6+29t4/384+t5/48+t6/384 Viceversa, quello di YçX è [1+(t+t2+ ... + t6)/6]/2 = ½+(t+t2+ ... +t6)/12 La formula di Faà di Bruno, che dà la derivata k-esima della composizione di due funzioni può essere trovata nel classico trattato An Introduction to Combinatorial Analysis di J.Riordan. Si noti che l'operazione ç tra v.a. è associativa e distributiva a destra. Sarebbe interessante studiare altre proprietà di tale operazione. 10. Il teorema di Watson Si può definire la potenza n-esima di una v.a. X secondo l'operazione somma aleatoria ponendo Xç n = X1+ X2+ ... +XX ovvero XçXç...çX n volte. Se x(t) è il p.g. di X, allora il p.g. di Xçn è la composizione n volte di x(t): x(t)çn = x(x( ... x(t))) n volte. Il seguente risultato, che dà un'applicazione della potenza su definita, è dovuto al reverendo H.W. Watson e pubblicato per la prima volta nel 1874. Sia X la v.a. che conta il numero di figli di un individuo (o le particelle emesse in una radiazione quando si frantuma un nucleo atomico (C.S.Everett-S.Ulam,1948)); sia poi pk la p. che un individuo faccia k figli. Se ogni figlio si riproduce come il padre (con la stessa distribuzione di p.) e indipendentemente dal padre e dai fratelli, qual è:
Si potrebbe dimostrare che se x(t) è la funzione generatrice di X, allora pn,k = Dkx(t)çn/k!|t=0 Inoltre la p. di estinzione vale 1 se <X>£ 1 altrimenti è la radice positiva, diversa da 1, dell'equazione in t: x(t) = t. Esempio Sia X la v.a. C(4) con polinomio generatore (1 + t + t2 + t3)/4 e <X> = 3/2. Così ogni padre può generare k figli con p. ¼, al variare di k = 0,1,2,3. Non è facile esprimere la p. pn,k ma la p. di estinzione si ottiene facilmente risolvendo l'equazione (1 + t+ t2 + t3)/4 = t; essa vale Ö 2-1. In pratica, per valutare la p. pn,k si utilizzano metodi Monte Carlo (cfr. M.Cerasoli-V.De Petris, http://www.vdepetris.it/Articoli.htm) Concludiamo qui questo lavoro ricordando solo che non ci sarebbe sufficiente spazio per illustrare i significati probabilistici della teoria delle matrici quadrate nell'ambito delle catene di Markov. Ad un altro articolo rimandiamo invece il compito di illustrare il significato probabilistico di concetti dell'analisi matematica. |