Michele Impedovo Articolo pubblicato su «La matematica e la sua didattica», n. 1 - 2000 Non insegnate agli studenti.
Introduzione Il calcolo infinitesimale è sempre stato considerato una tappa obbligata e uno scoglio nell'apprendimento della matematica. La computer algebra mette ora a disposizione dell'allievo strumenti di calcolo e di visualizzazione che rendono tale apprendimento più facile che in passato. Vorrei mostrare un percorso didattico che sfrutta le potenzialità della computer algebra per rendere più forti dal punto di vista semantico i concetti fondamentali, e per affiancare al tradizionale bagaglio teorico abilità di tipo algoritmico e padronanza nelle approssimazioni numeriche.
Un corto circuito Nel percorso tradizionale l'approccio allo studio di funzioni realizza una sorta di corto circuito didattico: la funzione più importante, che servirà da guida in ogni settore del calcolo infinitesimale, e cioè la funzione lineare non viene trattata. O meglio, viene trattata in geometria analitica come luogo di punti: la retta è caratterizzata da una equazione della forma Non è la stessa cosa: non distinguere tra funzione e luogo di punti trascina con sé perduranti equivoci.
Non a caso sorgono da subito confusioni sul fatto che alcune rette (quelle "verticali") sono più brutte delle altre, non rappresentano funzioni e non hanno il "coefficiente angolare". Se introduciamo la funzione lineare invece della retta geometrica non c'è confusione. Un modo assai interessante ed efficace di introdurre le funzioni lineari (e in generale le funzioni) consiste nell'utilizzare grandezze fisiche rilevate da sensori: esistono in commercio una grande varietà di sensori capaci di acquisire dati (di temperatura, di pressione, di intensità luminosa, di grandezze elettro-magnetiche, ¼) a intervalli regolari di tempo, e con una frequenza che può arrivare per alcuni sensori fino ai 10 kHz, dunque con una frequenza di campionamento impensabile con carta e penna. I dati rilevati dal sensore vengono elaborati da un interfaccia e trasmessi alla TI-92, che mediante un programma è in grado di ricavarne sia la tabella che il grafico. Per esempio utilizziamo un sensore di posizione: è in sostanza un sonar che manda ultrasuoni e ne riceve l'eco per riflessione da un ostacolo in moto; la misura dell'intervallo di tempo tra l'impulso emesso e quello riflesso viene tradotto in misura della distanza dell'ostacolo. Osserviamo il grafico posizione-tempo prodotto dal movimento di uno studente, al quale è stato chiesto di allontanarsi dal sensore con velocità costante (il grafico di una grandezza che varia in funzione del tempo è uno degli strumenti più forti dal punto di vista semantico per rendere solida l'idea di funzione). 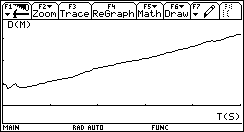 È evidente che non sarà possibile realizzare un moto in cui lo studente, nello stesso istante, si trovi in due posizioni differenti. Il grafico ottenuto non è certo una retta, ma, non sembri paradossale, è proprio il "riconoscere" una retta in quel grafico incerto a rendere più efficace la nozione di funzione lineare. Confondendo la retta geometrica con la funzione lineare si rischia di generare un equivoco che sarà difficile correggere in seguito: quando si lavora sul piano cartesiano con i classici problemi della geometria analitica il piano è rigidamente monometrico (è stata introdotta tacitamente la metrica euclidea), è proprio il piano geometrico della nostra intuizione spaziale, ed è quanto di più distante possa esserci dal piano della rappresentazione grafica di una funzione. Infatti quando si rappresenta una funzione le grandezze sui due assi sono solitamente non omogenee, le unità di misura scelte sui due assi sono arbitrarie e su tale piano non hanno alcun senso né la distanza né gli angoli. Occorre insegnare agli allievi a leggere le proprietà dei grafici delle funzioni non con occhio "metrico" ma con occhio "affine"; occorre leggere le proprietà che sono invarianti per dilatazione degli assi: il crescere, il decrescere, e successivamente il fatto che la rapidità di crescita stia a sua volta aumentando, diminuendo o rimanendo costante. Ecco che l'espressione "coefficiente angolare" si rivela addirittura sbagliata: che fine fa l'angolo se si misurano le distanze in centimetri anziché in metri? L'espressione corretta (e anche più corta) è "pendenza" (slope in inglese, pente in francese), che è un rapporto tra incrementi, e nulla ha a che fare con l'inclinazione della retta. L'approccio alle funzioni lineari invita in modo naturale ad una operazione che solitamente non viene svolta quando si ha a che fare con le rette della geometria analitica: l'analisi degli incrementi di una funzione. Ecco un piatto forte della preparazione scientifica: ricavare da una tabella di dati un modello convincente che li rappresenti. Nel caso del moto precedente analizziamo la tabella tempo-posizione (le posizioni sono rilevate dal sensore a intervalli uguali di circa 0.054 s). 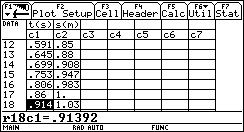 Ci accorgiamo del fatto che gli incrementi della distanza dal sensore (misurata in metri) sono, se si tralascia l'inizio del moto, circa costanti: non sorprenda, ma è proprio quel "circa" a rendere convincente la definizione di pendenza e a preparare il terreno per la ricerca della "miglior retta" che approssima n punti. Il metodo dei minimi quadrati deve diventare a mio parere un tema curricolare: dati n punti (xi,yi) e scelto il modello lineare x®ax+b, si tratta di determinare i parametri a e b che rendano minima la somma dei quadrati degli scarti di ciascun punto dalla retta y=ax+b. 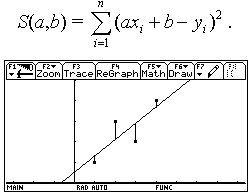 (il problema del perché si scelga "la somma dei quadrati degli scarti" e non "la somma degli scarti", oppure "la somma dei valori assoluti degli scarti" richiederebbe ben altro spazio; in proposito vedi Impedovo [4]). È possibile inizialmente affrontare il problema con carta e penna con pochi punti. Ecco un esempio. Determinare la funzione lineare che rende minima la somma dei quadrati degli scarti dai seguenti quattro punti: (1,1), (2,3), (3,2), (4,4). 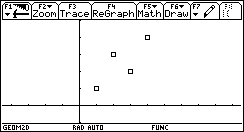 Memorizziamo la lista delle ascisse in xx e la lista delle ordinate in yy. La somma S(a,b) è un polinomio di secondo grado in a e b.  Per minimizzare S(a,b) non occorrono le derivate: se si pensa S come polinomio in a (e b come parametro), il grafico di S(a) è una parabola con la concavità verso l'alto; il valore di a che rende minimo S è l'ascissa del vertice. Analogamente per b. Si ottengono due relazioni lineari tra a e b. 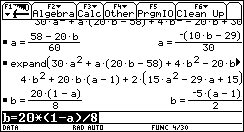 Risolvendo il sistema delle due equazioni si ottiene la soluzione: 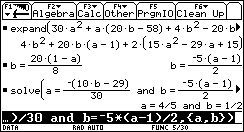 a=4/5, b = 1/2. La funzione lineare cercata è dunque: 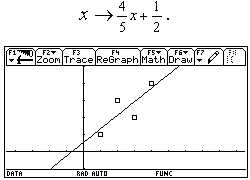 Svolto questo semplice esempio con carta e penna siamo autorizzati ad utilizzare le potenzialità della computer algebra. Ecco un esempio "scolastico": nella tabella seguente sono elencati, per i 21 studenti della mia classe di maturità dell'anno scolastico 97/98, la media dei voti in pagella al primo quadrimestre, e il successivo voto all'esame di maturità (l'ultima). 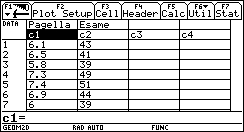 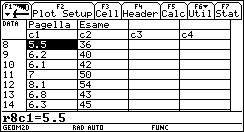 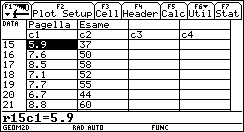 Ed ecco il corrispondente grafico per punti: in ascissa la media dei voti in pagella, in ordinata il voto d'esame. 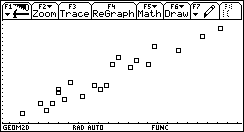 Come si vede la distribuzione sembra avere un andamento lineare; con la TI-92 (e in generale con un qualunque computer algebra system) è facile inserire i dati e ottenere subito l'equazione della retta di regressione. 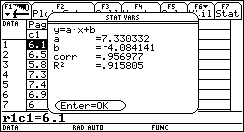 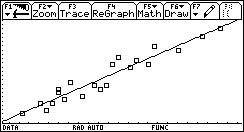 La funzione lineare che meglio approssima tali punti (secondo il modello dei minimi quadrati) è e si adatta abbastanza bene ai dati (il coefficiente di correlazione lineare vale circa 0.96). L'ultima osservazione riguarda le unità di misura: in geometria analitica non esistono unità di misura, mentre per le funzioni che solitamente rappresentiamo (e non solo in Fisica) esse hanno un forte valore semantico; la pendenza di una funzione lineare 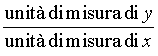 . .Nell'esempio precedente la pendenza 7.3 è misurata in "sessantesimi/decimi": con 1 punto in più nella media dei voti in pagella ci si può aspettare un voto di maturità maggiore di circa 7.3 punti; il termine noto -4.1 racconta invece qual è, in sessantesimi, l'improbabile voto d'esame per un candidato che si presentasse con una media dei voti uguale a 0. Riassumendo con uno slogan: più funzioni e meno geometria analitica. La pendenza (funzioni algebriche) Nell'approccio ai concetti di limite, di derivata e di integrale la computer algebra può migliorare radicalmente l'efficacia del nostro insegnamento. Questa, almeno, è stata la mia esperienza.
che approssima ¦'(x0) molto più efficacemente del solito rapporto incrementale. 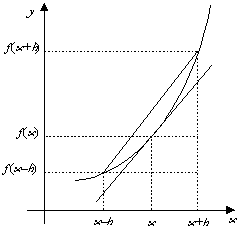 Definiamo dunque le funzioni ¦(x) e m(x,h) e calcoliamo m(2,h) con incrementi h via via minori.  Al tendere a zero di h la pendenza di ¦ in 2 tende a 12 (si osservi che l'errore è proporzionale al quadrato di h). Lo studente fornisce in modo naturale una sensata congettura: la pendenza di ¦ in 2 è 12. Anche il grafico, nel rettangolo di visualizzazione [0,3]´[0,27] risulta convincente. 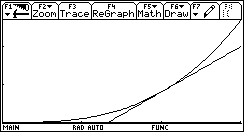 Il fondamentale vantaggio offerto dalle funzioni algebriche consiste nel fatto che tale congettura si può dimostrare: se si è data la definizione di retta tangente a ¦ in x0 come la retta che ha in x0 (almeno) due intersezioni coincidenti con y=¦(x), la dimostrazione è una semplice ed istruttiva applicazione del teorema di Ruffini. Infatti la retta di pendenza 12 passante per (2,¦(2)) ha equazione e l'equazione risultante del sistema 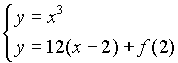 deve ammettere in x=2 due soluzioni, quindi il polinomio deve essere divisibile per (x-2)2.  Si ottiene, gratis, anche l'ulteriore punto di intersezione della retta tangente con il grafico di ¦: è il punto di ascissa -4. Dunque la pendenza di ¦ in 2 vale esattamente 12; poiché il "tendere" di m(x,h) a 12 quando h tende a 0 è evidente, si radica nello studente la fiducia in questo metodo di approssimazione. È possibile allora introdurre, in modo del tutto informale, l'idea di "limite": la funzione m(x,h) può diventare una funzione ad un solo argomento (x), perché per h abbastanza piccolo (per esempio 0.001) otteniamo una precisione ben superiore alle nostre esigenze (possiamo per esempio impostare a 3 il numero di cifre decimali visualizzate). La definizione di limite può essere rimandata al termine del percorso di scoperta, quando se ne sarà consolidato il valore semantico.  Senza lanciarsi in precoci generalizzazioni, si può ora guidare gli studenti alla scoperta e alla congettura: determinare la pendenza di ¦:x®x3 in 0, 1, 2, 3, 4, 5. 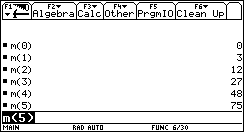 Non c'è studente che a questo punto non avverta, senza alcuna sollecitazione dell'insegnante, la necessità di generalizzare; ipotizzare quale sia la pendenza di ¦ in x0=6 è ora un gioco, a cui tutti partecipano. A parte il fatto che gli allievi sono più pronti di me a cercare e a trovare regolarità in una sequenza di numeri, in questa ricerca di generalizzazione si innesta quel lavoro utilissimo di cui si diceva: ricavare da una tabella di dati un modello che li rappresenti. Qui il modello è deterministico; si tratta di una funzione crescente, i cui incrementi (per Dx=1) non sono costanti ma sono costanti gli incrementi degli incrementi: L'unica funzione che ha questa caratteristica è la funzione quadratica In generale: le funzioni per le quali gli incrementi di ordine n, per Dx=1, sono costanti sono le funzioni polinomiali di grado n. È facile ricavare ora Inoltre possiamo fornire una dimostrazione di questo risultato generale, sempre con il teorema di Ruffini. L'equazione deve ammettere due soluzioni coincidenti con x0; se indichiamo con m la pendenza di ¦ in x0, il resto della divisione tra i polinomi deve essere il polinomio nullo. È il momento di utilizzare un programma che avevamo già sviluppato nell'ambiente di programmazione della TI-92: il programma quorem prende in ingresso due polinomi in x e fornisce in uscita il quoziente e il resto della divisione del primo per il secondo. A sua volta quorem sfrutta il programma coef che prende in ingresso un polinomio di grado n e fornisce in uscita la lista ordinata per grado decrescente degli n+1 coefficienti. 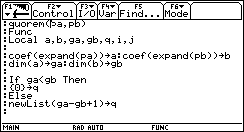   Il quoziente è quindi il terzo punto di intersezione tra la tangente e la curva è il punto di ascissa -2x0; il resto è il polinomio di primo grado in x in cui sia il coefficiente di x sia il termine noto si annullano (per qualunque x0) se e solo se Il passo successivo di generalizzazione può essere il seguente: approssimare la pendenza m(x) delle curve di equazione nel generico punto di ascissa x. Per esempio:  Si giunge in breve tempo alla generalizzazione: Da qui alla congettura più generale sulla funzione m(x) (che diventerà poi la funzione derivata) per un polinomio qualsiasi il passo è breve. Usiamo ancora il metodo di approssimazione per le funzioni 1/x e   Per 1/x la congettura sulla forma generale di m(x) non è difficile: e si può facilmente dimostrare con il teorema di Ruffini. Insisto nel dire che formulare congetture è per gli allievi un'attività molto stimolante e didatticamente importante, soprattutto per quelli più deboli, che sentono in qualche modo di poter padroneggiare la disciplina. Per anche per esponenti n negativi o razionali. Il fatto importante è che per curve algebriche ogni congettura può essere dimostrata o refutata: è sufficiente controllare se funzione e retta hanno due soluzioni coincidenti nel punto fissato. Per consolidare il concetto di pendenza è necessario ricorrere continuamente al grafico, e verificare i risultati via via ottenuti. Per esempio, se la pendenza di 1/x è -1/x2, allora nel punto di ascissa 2 la pendenza è -1/4, e l'equazione della retta tangente è 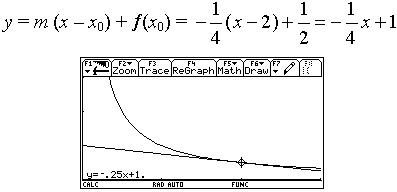 La pendenza (funzioni trascendenti) La definizione algebrica di retta tangente è inutilizzabile per le funzioni trascendenti, per le quali il concetto di molteplicità di uno zero non è recuperabile (se non sviluppando la funzione in serie di potenze). Diventa necessario quindi ricorrere ad una nuova definizione di retta tangente, che coinvolge necessariamente il concetto di limite. È qui che il metodo di approssimazione svolge un ruolo fondamentale per avvicinare gli studenti alla definizione di limite, che verrà definita solo più avanti.
 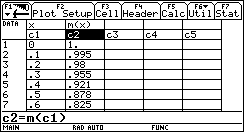 Tracciamo ora il grafico per punti di m(x) e confrontiamolo con il grafico di sin(x). 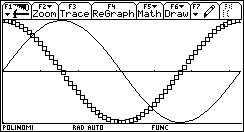 Non è difficile congetturare che la derivata di sin(x) sia cos(x). Un lavoro analogo può essere svolto per la funzione ¦(x)=ln(x). 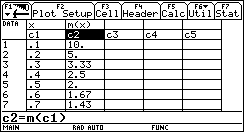 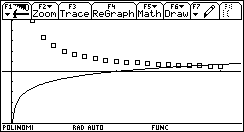 In quest'ultimo caso la tabella, più del grafico, dà una indicazione chiara per formulare l'ipotesi che la derivata di ln(x) sia 1/x. È un'ipotesi che può essere verificata con la precisione desiderata. Questa attività di approssimazione della pendenza di una funzione può e deve essere svolta per ogni nuova funzione analizzata: in un certo senso è proprio la pendenza che caratterizza in modo significativo una curva. L'attività di approssimazione fornisce un metodo generale di indagine e consolida concetti che potranno essere resi sistematici in seguito. Un problema di area
1) L'esigenza di misurare l'area sottesa dal grafico di ¦(x) nell'intervallo [a,b] può nascere dalla necessità di misurare la bontà con cui una funzione polinomiale approssima una funzione trascendente. Per esempio, approssimiamo Nell'intervallo [0,p/2] con la parabola y =g(x) che ha vertice in (p/2,1) e passa per l'origine. Risulta Il grafico della parabola è punteggiato). 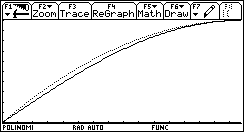 Egrave; buona l'approssimazione? "Quanto" è buona? È intuitivo che un modo di misurare la "distanza" tra le due funzioni consiste nel calcolare il rapporto tra l'area della regione di piano compresa tra esse, e l'area sottesa da sin(x). 2) Un altro approccio all'integrale è dato dalla necessità di definire in modo convincente il valore medio di una funzione ¦(x) continua in un intervallo [a,b]. Per esempio, immaginiamo un termografo che tracci, in un intervallo di tempo Dt il grafico della temperatura. Come definire la temperatura media in quell'intervallo? È interessante proporre agli studenti un confronto fra funzioni che abbiano gli stessi valori iniziale e finale, e che crescano in modo differente. Per esempio, qual è la funzione che ha il valore medio maggiore tra quelle mostrate nel seguente grafico? 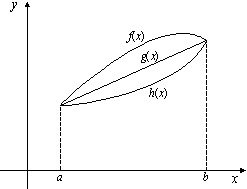 La discussione con gli allievi mette in luce livelli di comprensione differenti della "lettura" di un grafico; non sono pochi coloro che insistono nel sostenere che le tre funzioni hanno lo stesso valore medio, che è uguale alla media dei valori iniziali e finali. Interpretando i grafici come andamento del mio stipendio in funzione del tempo qualcuno ammette che lo stipendio ¦(x) è il più desiderabile in quell'intervallo. 3) Un altro modo di introdurre il tema degli integrali consiste nel proporre a sorpresa, senza alcun nesso con gli argomenti svolti fino a quel momento, il seguente lavoro di gruppo, che solitamente scatena una forte competizione. Osserva il grafico seguente, relativo alla funzione x®1/x: approssima al meglio l'area della regione ombreggiata. 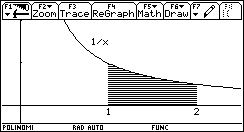 Il comportamento degli alunni in questa situazione è davvero interessante; innanzitutto nessuno ha dubbi sul significato del testo, e nessuno pone il problema epistemologico della definizione di area delimitata da un tratto di curva. L'area c'è, e si vede: è uno dei concetti più forti che gli alunni possiedono. È interessante notare che molti gruppi si orientano spontaneamente verso il classico "metodo dei rettangoli": dividono l'intervallo [1,2] in 5 o 10 intervalli, e calcolano l'area dei rettangoli inscritti, o circoscritti; qualche gruppo usa addirittura i trapezi. Una breve discussione al termine dei lavori conduce a questa idea da tutti condivisa: per approssimare l'area richiesta si può dividere l'intervallo [a,b] in n intervalli di ampiezza si calcola il valore della funzione ¦(x) nei punti di suddivisione si calcolano le aree dei rettangoli di base Dx e altezza ¦(a+kDx), e infine si sommano: 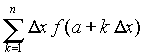 . .Si passa subito all'implementazione del relativo algoritmo. Il programma area usa la funzione ¦(x), prende in ingresso gli estremi a, b dell'intervallo e il numero n di intervalli. 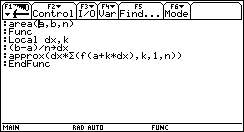 Ecco il programma area applicato a sin(x) nell'intervallo [0,p/2]. 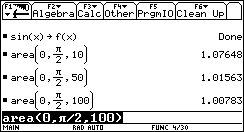 Ipotizziamo che al crescere di n l'area sottesa dalla sinusoide tra 0 e p/2 si avvicini a 1. Possiamo ora risolvere in forma numerica il problema di valutare la bontà con cui approssima f(x) = sin(x).  L'errore medio è inferiore al 5%. Vogliamo ora iniziare un'attività di ricerca sperimentale. Cominciamo l'analisi dalle funzioni più semplici; sia ¦: x®x2. 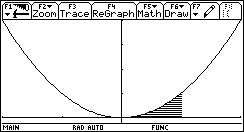 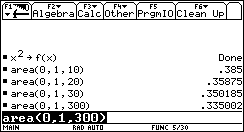 Come si vede l'algoritmo converge molto lentamente. Possiamo migliorarlo, come subito qualcuno suggerisce, utilizzando i trapezi anziché i rettangoli. L'approssimazione è allora data da 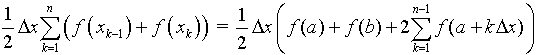 Aggiorniamo il programma area.  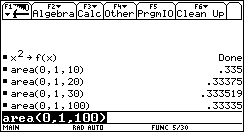 L'algoritmo converge più rapidamente. Possiamo ipotizzare senza difficoltà che l'area sottesa da x2 nell'intervallo [0,1] valga 1/3; d'altra parte il teorema di Archimede conferma questo risultato. Ci siamo quindi dotati di uno strumento potente, con il quale si può iniziare un lavoro di ricerca. Indichiamo con l'area sottesa dalla funzione continua (e positiva, per ora) ¦ nell'intervallo [a,b]; La notazione di Leibniz 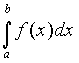 è proprio sgradevole ad un primo approccio, e d'altra parte non è certo nata con intenti pedagogici; varrebbe la pena sostituirla con altre notazioni più efficaci dal punto di vista didattico. Possiamo ora formulare una congettura su quale sia un'espressione generale per Approssimiamo le aree sottese da x2 negli intervalli [0,1], [0,2], [0,3], [0,4]. 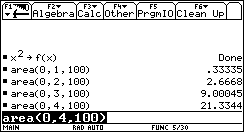 Si ottiene in modo molto convincente la relazione e più in generale In modo analogo possiamo porci il problema dell'area sottesa da ¦(x)=x3. 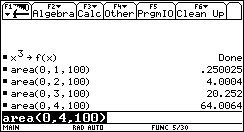 e arrivare al risultato Ancora, con ¦(x)=x4: 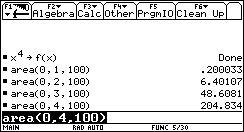 si ottiene Anche lo studente meno fantasioso nota a questo punto la regolarità, e propone la legge generale che avvicina qualcuno all'intuizione del teorema fondamentale. È utile a questo punto svolgere un po' di calcolo simbolico, che può consolidare ulteriormente il concetto di limite. Per ottenere un'approssimazione di int(x2,a,b) possiamo calcolare in forma simbolica e aumentare indefinitamente n. Senza perdere in generalità possiamo porre a=0.  Ora si tratta di capire che cosa accade all'espressione quando n diventa via via più grande: gli allievi reagiscono bene alla sollecitazione, e danno per buono il fatto che "quando n diventa infinito allora 1/n2 diventa zero". Possiamo sfruttare l'occasione per iniziare a utilizzare la notazione di limite:   Naturalmente per le funzioni trascendenti questi calcoli simbolici non conducono a risultati utili. Si tratta ora di introdurre la funzione integrale, per intravedere il teorema fondamentale del calcolo e legare il concetto di derivata a quello di integrale. Per far ciò, occupiamoci di ¦(x)=sin(x). Nell'intervallo [0,2p] approssimiamo con il programma area l'integrale con x = 0, 0.1, 0.2, ¼, 2p. 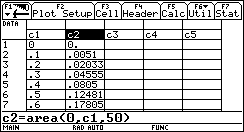 Costruiamo così, per punti, la funzione integrale Possiamo confrontare questa funzione con la funzione seno. 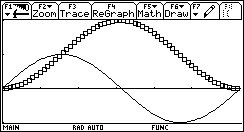 Osserviamo che ¦ ha uno zero dove g ha un massimo, che ¦ ha un massimo dove g ha un flesso, che ¦ è positiva dove g è crescente, che ¦ è negativa dove g è decrescente: insomma, ci sono tutti gli ingredienti per ipotizzare che ¦ sia la derivata di g. Un altro modo per ottenere lo stesso grafico più agevolmente consiste nell'utilizzare la funzione predefinita nInt della TI-92, che calcola in modo molto efficiente l'integrale definito, e la cui sintassi è mostrata nella figura seguente. 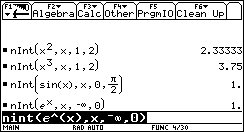 Possiamo sfruttare tale funzione nell'ambiente Y=Editor, definendo in y1(x) la funzione seno, e in y2(x) direttamente la funzione integrale nInt(sin(t),t,0,x). Il grafico (tracciato per punti: 1 punto ogni 5 pixel) coincide naturalmente con quello già ottenuto con la nostra funzione area.  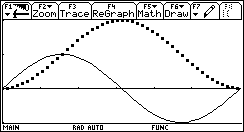 Chiediamoci ora: qual è la derivata della funzione integrale implementata in y2(x)? Utilizziamo il comando predefinito nDeriv, analogo a nInt, definendo in y3(x) la derivata di y2(x), e tracciamone il grafico (1 punto ogni 10 pixel). 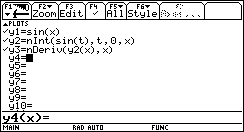 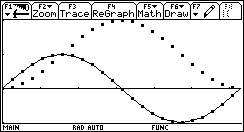 Insomma, è abbastanza eccitante "vedere" che il grafico della derivata della funzione integrale di sin(x) coincide con sin(x)! Il teorema fondamentale non è mai stato, nella mia lunga carriera di insegnante, così vivo. C'è di più: possiamo visualizzare il grafico di funzioni che non abbiamo mai visto! È noto infatti che esistono funzioni la cui funzione integrale non è esprimibile come funzione elementare. Una di queste è (purtroppo) la celebre funzione di Gauss Possiamo finalmente toglierci il gusto di tracciare il grafico di 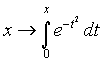 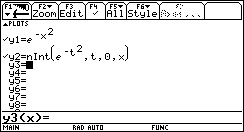 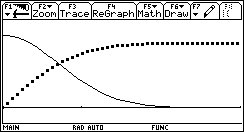 Oppure possiamo finalmente "vedere" come il grafico di un'altra celebre funzione integrale: 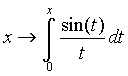 oscilli intorno a p/2! 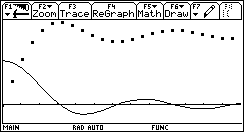 Al termine di questo percorso (ma solo al termine) illustro agli studenti la sintassi del simbolo ò sulla TI-92, mostrando loro che ciò che ci serve (integrale definito e indefinito) è già implementato in forma simbolica. 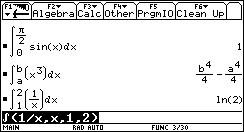 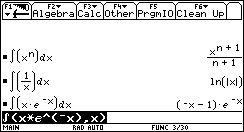 Gli alunni mostrano un certo salutare disappunto di fronte a questa scoperta: "Ma come, allora le funzioni e gli algoritmi che abbiamo costruito noi non servono più a nulla?". Sono serviti, eccome: tale disappunto ne è la prova evidente. Conclusioni L'utilizzo della computer algebra in tutte le sue articolazioni (calcolo approssimato, calcolo simbolico, definizione di funzioni, costruzione di algoritmi, grafici, tabelle) costituisce uno strumento didattico formidabile per rendere più vivi, più ricchi, più precisi i concetti matematici. Naturalmente la fase di esplorazione e di congettura non esaurisce il lavoro didattico, ma certamente ne può costituire l'ossatura portante. Uno dei successi che ho registrato in questo lavoro riguarda gli alunni più deboli, che hanno mostrato un aumento di interesse e di fiducia in se stessi; la possibilità di controllare i risultati, e soprattutto il vedere una matematica che non è già codificata (avvicinabile solo con spirito dimesso) si è dimostrato essere un forte stimolo. Infine la padronanza algoritmica dimostrata dagli studenti è sorprendente: nati con il telecomando in mano, gli studenti del 2000 mostrano di padroneggiare la TI-92 spesso meglio del loro insegnante. Anche questo stimola ad una fiducia in se stessi che apre le porte alla passione per lo studio e per la conoscenza. Bibliografia [1] C. Dodson, E. Gonzales, "Experiments in mathematics using Maple", Springer
|