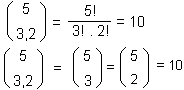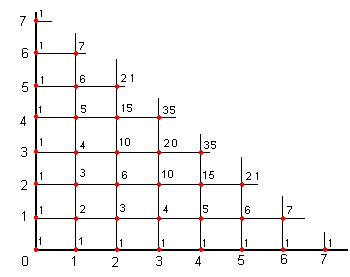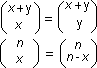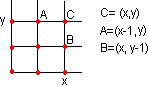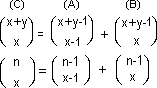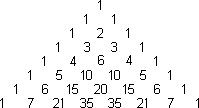Consideriamo ancora il modello delle biglie e delle scatole per proporre un problema di tipo combinatorio. Supponiamo di avere 5 scatole e 5 biglie. Vogliamo collocare qualcuna delle biglie nelle scatole, in modo che una scatola contenga al più una biglia.

Indichiamo con A le scatole che contengono biglie e con B quelle che non ne contengono. Le 5 scatole diventano così una parola di 5 lettere prese dall'alfabeto {A, B}.

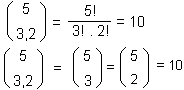
Il problema di trovare in quanti modi le biglie possono essere collocate nelle scatole, diventa così quello di trovare quanti anagrammi ci sono in ciascuna parola di 5 lettere prese dall'alfabeto {A,B}. In quanti modi si possono collocare 3 biglie in 5 scatole? Il calcolo è indicato nella formula a lato. Abbiamo già visto al §8 che vi è una corrispondenza biunivoca tra permutazioni di due elementi il primo ripetuto k volte e il secondo (n-k) volte e combinazioni di n elementi di classe k o (n-k).

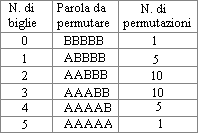
Tenendo presente tale corrispondenza, proviamo a calcolare in quanti modi si possono collocare le biglie nelle 5 scatole, variando di volta in volta il numero delle biglie: E' facile riscontrare che il numero delle permutazioni calcolato nella tabella è esattamente uguale a quello delle combinazioni di n elementi di classe k, con n = 5 e k che varia da 0 a 5. Il numero totale delle permutazioni coincide con quello delle disposizioni con ripetizione di 2 elementi di classe n (le lettere A e B prese, con ripetizione, n la volta), che sono 2n. Nel nostro caso, avendo 5 elementi, le disposizioni saranno in tutto 25 = 32.

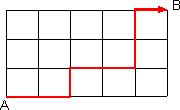
Una situazione molto simile a quella appena esaminata si presenta nello schema qui a lato. In esso si parte dal punto A e, seguendo le linee della griglia, s'arriva al punto B. Il percorso minimo è quello costituito da 5 passi verso destra e 3 verso l'alto, in qualunque ordine siano compiuti. Si possono scegliere perciò tanti percorsi diversi, quanti sono tutti gli anagrammi della parola DDDDDAAA, che sono 56. L'esempio di percorso qui a lato corrisponde alla parola DDADDAAD.

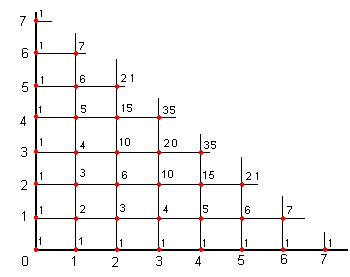
Vogliamo generalizzare un po' il problema, realizzando un reticolo a maglie quadrate (reticolo di Polya).Su tale reticolo si calcolano i numeri dei percorsi minimi per andare dal punto (0,0) fino ad un punto (x, y), posto in uno qualsiasi dei nodi del reticolo. Per andare dal punto (0,0) al punto (0,0) c'è un solo modo: restarci! Il numero di percorsi per raggiungere gli altri punti del reticolo sono indicati in corrispondenza degli stessi. Essi sono stati calcolati determinando il numero di passi a destra (D) e in alto (A)a partire da (0,0) per arrivare fino al punto considerato e poi contando gli anagrammi della parola formata da altrettante lettere D e A. Ciascun anagramma costituisce infatti un possibile percorso alternativo per giungere alla meta designata. Si può anche calcolare il numero di combinazioni di (x+y) elementi di classe x, o (x+y) elementi di classe y. Nello schema si vede che i valori simmetrici rispetto alla diagonale sono uguali. Pertanto il numero di percorsi per andare ad un punto (x, y) o ad un punto (y, x) è lo stesso.

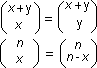
Si dimostra così l'uguaglianza indicata nelle formule qui a lato. La prima non è altro che la conseguenza di quanto abbiamo appena osservato. La seconda si ottiene dalla prima, sostituento n a (x + y). Tale uguaglianza, oltre che giustificare la simmetria tra i percorsi posti nello schema precedente, è utile per eseguire il calcolo delle combinazioni per la via più breve. E' preferibile calcolare le combinazioni di 8 elementi di classe 3, piuttosto che quelle di 8 elementi di classe 5, che richiedono fattoriali più grandi. Lo schema precedente è utile per fare un'altra considerazione.

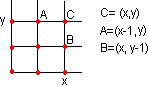
Prendiamo tre caselle contigue, contrassegnandole con le lettere A, B, C, e scriviamo le rispettive coordinate. Quanti percorsi vi sono per raggiungere una delle tre posizioni indicate con A, B e C? Osservando attentamente lo schema, è facile arrivare alla seguente conclusione che, per andare in C, occorre passare necessariamente per A o per B. Di conseguenza, il numero di percorsi per arrivare a C sarà uguale alla somma di quelli per andare ad A e di quelli per andare a B. Si ha cioè:

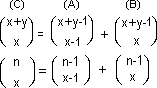
Questa formula permette di calcolare in modo ricorsivo i numeri nello schema. Basta sommare i valori posti a sinistra e al di sotto del numero da calcolare. Proviamo ora a compiere una rotazione dello schema (eliminando il reticolo e lasciando solo i numeri). Ci apparirà il ben noto triangolo di Pascal.

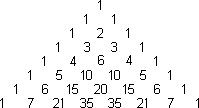
Il triangolo presenta talune caratteristiche molto interessanti. I suoi valori, come abbiamo visto, si possono ottenere per via ricorsiva, sommando i due termini posti immediatamente al di sopra del numero da calcolare. Si tratta della nota proprietà di Stifel, usata da tutti gli studenti per costruire ricorsivamente le varie righe del Triangolo. I valori, in ogni caso, si possono calcolare direttamente, per mezzo delle combinazioni di n elementi di classe k. Basta porre n = numero di riga, e k = numero d'ordine di ciascun elemento di una riga a partire da 0. Il triangolo di Pascal (noto in Italia come triangolo di Tartaglia) è usato, fra l'altro, per calcolare i coefficienti dei termini che si ottengono sviluppando la potenza del binomio (a + b)n. Per tale ragione, il simbolo 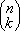delle combinazioni viene anche denominato coefficiente binomiale

Fra le innumerevoli proprietà del triangolo di Pascal, alcune sono molto utili per comprendere molte delle proprietà del calcolo combinatorio:

• I due termini estremi di ogni riga hanno valore 1, poiché corrispondono rispettivamente ai due coefficienti binomiali:
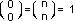
• I termini simmetrici di una riga sono uguali, per la proprietà già vista nel precedente reticolo di Polya.
• A partire dalla seconda riga, un qualsiasi termine è dato dalla somma dei due termini posti immediatamente al di sopra di esso(*).
• La somma dei valori di una riga ennesima è sempre uguale a 2ⁿ, per la ragione già vista in precedenza (biglie nelle scatole).