2.3 Eventi dipendenti ed indipendenti.

E' bene a questo punto precisare meglio il concetto di dipendenza o indipendenza tra due eventi.
L'indipendenza può essere logica o intuitiva quando tra gli eventi non c'è nesso plausibile. Immaginiamo due eventi:
A: "Il primo estratto sulla ruota di Genova è il 65."
B: "A L'Aquila la temperatura notturna è scesa sotto lo zero."
E' del tutto evidente che la temperatura notturna a L'Aquila è assolutamente indipendente dal numero estratto sulla ruota di Genova e viceversa. I due eventi sono quindi indipendenti fra loro. Non sempre le cose sono così chiare. Sono molti i fenomeni privi di collegamenti logici, che si rivelano connessi in qualche misura. Ne sono esempio molte statistiche mediche che mettono in relazione alcuni tipi di alimenti con il rischio d'infarto o il fumo di sigarette con il rischio di tumore ai polmoni. Le compagnie di assicurazione hanno evidentemente stabilito un nesso tra la residenza dell'automobilista e il rischio di provocare incidenti (o di ... dichiararli), se hanno fissato premi più costosi per i cittadini di alcune zone rispetto a quelli di altre. Viceversa, si possono avere casi in cui due eventi sembrano dipendere l'uno dall'altro, ma il calcolo delle probabilità permette di verificare che sono indipendenti.
Esempio. Gettiamo due dadi uno rosso ed uno bianco e consideriamo i seguenti due eventi:

1. il dado rosso presenta la faccia 6 (p=1/6)
2. i due dadi presentano facce uguali (p= 6/36 = 1/6)

Nel lancio di due dadi, lo spazio campione è costituito da 36 coppie di dadi. Tuttavia il verificarsi dell'evento A, riduce lo spazio campione ai soli sei casi in cui il dado rosso presenta la faccia 6.

In tale situazione c'è un solo caso con due facce uguali: (6, 6); quindi la probabilità di B, sapendo che A si è verificato, è 1/6.

Anche nel caso che non si sia verificato l'evento A la situazione non cambia, poiché lo spazio campione (vedi la figura dell'esercizio 1.4) si riduce a 30 casi e fra essi 5 sono quelli con due facce uguali, quindi p(B)= 5/30 = 1/6.
Come si vede, sia che A si sia verificato, sia nel caso contrario, la probabilità di B resta sempre 1/6.
E' altrettanto facile verificare che non viene modificata la probabilità di A supponendo che si sia verificato oppure no l'evento B. I due eventi sono quindi da considerare fra loro indipendenti.
Introduciamo un nuovo simbolo p(A|B), che si legge "probabilità dell'evento A noto che sia l'evento B", cioè la probabilità che assume l'evento A, sapendo (o supponendo) che B si sia verificato.

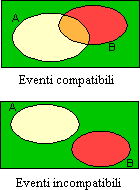
In genere si calcola tale probabilità attraverso un restringimento dello spazio campione, indicato dal rettangolo verde, al solo insieme che rappresenta l'evento A ed andando a trovare il rapporto rispetto ad esso della parte di A ancora favorevole a B (area arancione). In pratica si tratta di calcolare il rapporto tra la probabilità dell'intersezione AÇB e la probabilità dell'insieme A. Abbiamo cioè p(B|A) = p(AÙB)/p(A).    (4) Nel caso di eventi indipendenti si ha p(B|A)=p(B).

Dalla relativa figura si evince anche che, se si tratta di eventi incompatibili, allora p(B|A) è nulla, poiché i due elementi hanno intersezione vuota e quindi il numeratore della (4) vale 0. Dalla (4) si ricava che

 

p(AÙB) = p(A) × p(B|A).     (5)
eventi dipendenti
La (5) vale ovviamente anche per gli eventi indipendenti, in cui (B|A) è uguale a p(B), ma in tal caso è più semplice usare la (3).

Esercizio 2.5 Prendi una moneta da 1 euro (la cifra è scritta da una sola parte) e un dado. Lancia entrambi e calcola la probabilità di avere 1 sia sulla moneta che sul dado.
Abbiamo i seguenti due eventi.

1. Sulla moneta appare il valore 1 (p=1/2)
2. Sul dado appare il valore 1 (p=1/6)

I due singoli eventi sono indipendenti. Per la (3), la probabilità dell'evento composto (A Ù B) è data dal prodotto delle due probabilità:
(1/2) × (1/6) = 1/12.

Esercizio 2.6 Si prendano due carte da un mazzo da poker. Calcola la probabilità di avere una coppia di assi.
L'evento si compone dei due eventi singoli:

1. la prima carta è un asso
2. la seconda carta è asso.

I due eventi non sono indipendenti, poiché l'estrazione della prima carta modifica lo spazio campione, in cui resta una carta in meno.
Abbiamo p(A)= 4/32 = 1/8 (ci sono 4 assi nelle 32 carte da poker) e p(B|A) = 3/31 (restano solo 3 assi nelle 31 carte rimaste). Quindi, per la (5) si ha p(AÙB) = (1/8) × ( 3/31) = 3/248.

 

Esercizio 2.7 Considera lo spazio campione rappresentato dall'intero rettangolo di area a∙b della figura a lato. Fissa due eventi: A: "Un punto preso a caso nello spazio campione appartiene alla superficie tratteggiata in blu" B: "Un punto preso a caso nello spazio campione appartiene alla superficie tratteggiata in verde". I due eventi sono indipendenti? Calcoliamo le probabilità dei due eventi, in base al rapporto tra l'area considerata e quella dello spazio campione:

p(A) = (a∙d)/(a∙b) = d/b
p(B) = (c∙b)/(a∙b) = c/a
p(A) ∙ p(B) = (d/b) ∙(c/a) = (c∙d)/(b∙a)

Calcoliamo la probabilità dell'evento (AÙB) indicato dall'area tratteggiata sia in verde che in blu:
p(AÙB)= (c∙d)/(b∙a)
La probabilità dell'evento (AÙB) è uguale al prodotto delle probabilità di A e di B, quindi i due eventi sono indipendenti.

 

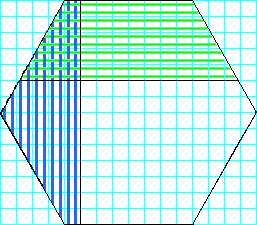
Esercizio 2.8 Considera lo spazio campione rappresentato dall'intero esagono della figura qui a lato e la cui area misura 168 caselle . Fissa due eventi: A: "Un punto preso a caso nello spazio campione appartiene alla superficie tratteggiata in blu" B: "Un punto preso a caso nello spazio campione appartiene alla superficie tratteggiata in verde" I due eventi sono indipendenti? La superficie blu ha un'area di 42 caselle e quella verde di circa 57,857 caselle. Dunque p(A)= 42/168 e p(B)=57,857/168. Moltiplichiamo le due probabilità: p(A)∙p(B) = (42/168) ∙(57,857/168) = circa 0,086.

La superficie tratteggiata sia in verde che in blu ha un'area di circa 13,928.
Dunque p(AÙB)= 13,928/168, circa 0,0829.
La probabilità dell'evento (AÙB) è diversa dal prodotto p(A)∙p(B), quindi i due eventi non sono indipendenti.
Esercizio 2.9 Considera i due eventi dell'esercizio 2.8 e calcola le probabilità di (A|B) e di (B|A), confrontandole con le rispettive probabilità degli eventi A e B.
Per la (4) si ha:
p(A|B) = (13,928/168)/(57,857/168) = 13,928/57,857 = ~ 0,24, che è minore di p(A) che vale 0,25.
p(B|A) = (13,928/168)/(42/168) = 13,928/42 = ~ 0,33, che è minore di p(B) che vale ~ 0,34.

 

Esercizio 2.10 In un consiglio comunale alla lista di maggioranza è andato il 60% dei seggi e a quella di opposizione il restante 40%. I consiglieri di maggioranza sono per il 60% uomini e per il 40% donne. I consiglieri di opposizione, invece, sono per il 70% uomini e per il 30% donne. Vedendo entrare in consiglio una donna, qual è la probabilità che appartenga al partito di maggioranza? Nella situazione appena descritta possiamo definire i seguenti due eventi: A: "E' un consigliere donna" B: "E' un consigliere della maggioranza"

La probabilità che si chiede di calcolare è quindi quella dell'evento (B|A), cioè quella che il consigliere "sia della maggioranza sapendo che è donna".
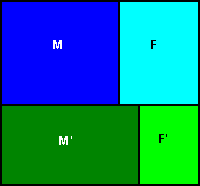
La situazione può essere analizzata con una tabella suddivisa in quattro aree. La riga orizzontale suddivide lo spazio campione in due zone: quella superiore azzurra che rappresenta i consiglieri di maggioranza (60%) e quella inferiore verde, che rappresenta l'opposizione (40%). I consiglieri di maggioranza sono a loro volta suddivisi in una zona azzurro scuro che indica i maschi (60%) e una azzurro chiaro che indica le donne (40%). Analogamente i consiglieri maschi di opposizione sono indicati con una zona verde scuro (70%) e con una zona verde chiaro le donne (30%).
Abbiamo già visto che nella probabilità condizionata occorre operare un restringimento dello spazio campione. Nel nostro caso si tratta quindi di restringiere lo spazio campione alle due parti più chiare, corrispondenti all'evento A (consigliere donna). La probabilità cercata sarà data dal rapporto tra l'area azzurro-chiaro (donne di maggioranza) e l'intera area chiara (donne di maggioranza più donne di opposizione).
La zona azzurro chiaro F rappresenta il 40% del 60% del campione: (40/100).(60/100) = 24/100.
La zona verde chiaro F' rappresenta il 30% del 40% del campione: (30/100).(40/100)= 12/100.
Le donne nel consiglio comunale sono quindi pari alla somma F + F' = 24/100 + 12/100 = 36/100.

La probabilità cercata è quindi data dal rapporto tra le donne della maggioranza F e il totale delle donne (F + F'):