4.2 Valore medio di una variabile aleatoria.

La media aritmetica di una successione di numeri si ottiene sommando tutti i numeri e dividendo per il numero di termini sommati. Esempio:

m(3,8,10) = (3+8+10)/3 = 7.

Anche per una variabile aleatoria, se tutti i numeri avessero la stessa probabilità, la media sarebbe data dalla loro somma, divisa per il numero di termini. Ad esempio, la media dei numeri di un dado è (1+2+3+4+5+6)/6 =21/6=3,5.
Non sempre i termini di una variabile aleatoria hanno la stessa probabilità. La media aritmetica dev'essere sostituita allora dalla media ponderata, usando come pesi dei vari termini, le rispettive probabilità.
La media ponderata si calcola sommando i prodotti di ciascun termine per il proprio peso e dividendo per la somma dei pesi. Ad esempio, in una classe di 20 alunni l'altezza media è 1,62 e in un'altra di 28 alunni l'altezza media è 1,68. Sommando le due classi l'altezza media sarà

 


Le altezze 1,62 e 1,68 sono i valori e 20 e 28 sono i relativi pesi.
Applicando tale procedimento alle variabili aleatorie, la formula diventa un po' più semplice, poiché al denominatore la somma dei pesi assume il valore 1 (somma di tutte le probabilità) e quindi si omette. Rimane il solo numeratore, che contiene la somma dei valori della prima riga moltiplicati per le rispettive probabilità.

 

m(v.a.) = v1 p1 + v2 p2 + ... +vn pn

Esercizio 4.1 Una coppia di sposi spera di avere un figlio maschio, per non far estinguere il cognome del marito non essendoci altri parenti maschi sposati. Quattro figli di questi tempi sono troppi, perciò decidono di fare al massimo tre tentativi. Se nasceranno tre femmine, perciò non vi saranno ulteriori tentativi. Trova il numero medio di figli e di maschi che avrebbero le famiglie se tutte facessero la stessa scelta.
Gli eventi possibili sono:
M con probabilità 1/2
FM con probabilità (1/2)2 = 1/4
FFM con probabilità (1/2)3= 1/8
FFF con probabilità (1/2)3= 1/8

La coppia potrà avere da uno a tre figli. Il numero di maschi può essere invece 1 nei primi tre eventi oppure 0, nel quarto evento. La probabilità che nasca un maschio è (1/2) + (1/4) + (1/8) = 7/8. Quella che non nascano maschi è 1/8.
Abbiamo così le seguenti due variabili aleatorie, la prima sul numero totale di figli e la seconda sul numero di maschi.
La media della v.a. è: 1∙ (1/2) + 2 ∙ (1/4) + 3 ∙ (1/4). Ogni famiglia ha in media 7/4 di figli. Non potendo tagliare in quarti i figli, il valore significa che nascono in media 7 figli ogni 4 famiglie, se tutte fanno la stessa scelta della nostra coppia.
La media della v.a. è 0 ∙ (1/8) + 1 ∙ (7/8) = 7/8 Il numero medio di maschi è esattamente la metà del numero medio di figli. L'altra metà saranno ovviamente femmine. Ciò significa che, pur desiderando figli maschi, finiranno per nascere tanti maschi quante femmine, esattamente 7 maschi e 7 femmine per ogni 8 famiglie.

Esercizio 4.2 - Il gioco dei tre dadi Si tratta di un gioco assai diffuso nel medioevo. Su un grande tavolo è disegnato un rettangolo diviso in 6 quadrati, numerati da 1 a 6. Il banco invita gli spettatori a puntare su uno dei sei numeri. Terminate le puntate, il banco getta tre dadi. Chi ha puntato sul numero uscito in uno qualsiasi dei tre dadi vince il valore della somma puntata. Se il numero è presente su due dadi la vincita si raddoppia. Se la "fortuna" fa uscire il numero su tutte e tre le facce, la vincita si triplica.

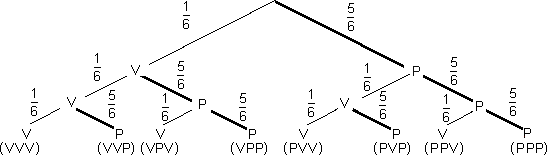
Ogni giocatore è convinto di arricchirsi, pensando:

"Con un dado ho una probabilità su sei di vincere. Con tre dadi la probabilità diventa il triplo, cioè 3 su 6 (*). In pratica vinco o perdo con la stessa probabilità. Alla lunga dovrei andare in pari. Ma siccome ogni tanto mi capiterà di vincere il doppio della posta o addirittura il triplo, credo proprio che mi farò un bel gruzzolo!".

E dai a giocare, dimenticando una regola fondamentale: mai scommettere contro un professionista, che va in giro per le feste non per regalare soldi alla gente, ma solo per arricchirsi alle spalle degli ignoranti. Ma dove sta il trucco? Certo non nei dadi, ché altrimenti qualcuno finirebbe per scoprire il numero che esce più di frequente e punterebbe su di esso, questa volta sì a danno del banco.

________
(*) Il ragionamento è errato. La probabilità di vincere una volta con tre dadi non è il triplo di quella che si ha con un dado, come già aveva osservato dal cavaliere di Meré. Molte persone ignoranti non se ne rendono conto ed è sulla loro ignoranza che fanno affidamento coloro che propongono i giochi.

Per risolvere l'arcano non resta dunque che costruire un bel grafo ed analizzare tutti i possibili esiti.
La probabilità di vincere per ogni dado è 1/6. Quella di perdere è 5/6. Si hanno 4 possibili eventi:
  • Vincere tutte e tre le volte: (VVV) = con probabilità(1/6)3 = 1/216;
  • Vincere due volte: (VVP), (VPV), (PVV) = con probabilità [(1/6)(1/6)(5/6)] × 3 = 15/216,
  • Vincere una sola volta: (VPP),(PVP),(PPV), con probabilità [(1/6)(5/6)(5/6)]× 3 = 75/216;
  • Perdere tutte e tre le volte: (PPP) (5/6)3 125/216;

Dai risultati ottenuti per ciascuno degli eventi si può ricavare la seguente variabile aleatoria, in cui, con un piccolo strappo alla regola, introduciamo il valore negativo -1 per la perdita.


Il valore medio della nostra variabile casuale è

3 × (1/216) + 2 × (15/216) + 1 × (75/216) - 1 × (125/216) = -17/216

Il giocatore perde in media 17 volte la posta ogni 216 partite, quindi il banco vince in media circa il 7,87 % del totale delle giocate. Non si tratta di piccoli guadagni, poiché molti presenti sono invogliati a puntare dalle grida di coloro che vincono (ce n'è sempre qualcuno), mentre di solito chi perde tace!